题目内容
长均为L,质量均为m的两根均匀直杆A,B,它们的上端用光滑铰链铰接,悬挂于天花板上,在距离两杆下端点均为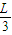 处,用光滑铰链M、N与弯杆C铰接,A,B两杆被弯杆C撑开的角度为2θ,弯杆C、铰链的质量均不计,如图所示,则可知弯杆C对杆A的作用力的方向为 ,大小为F= .
处,用光滑铰链M、N与弯杆C铰接,A,B两杆被弯杆C撑开的角度为2θ,弯杆C、铰链的质量均不计,如图所示,则可知弯杆C对杆A的作用力的方向为 ,大小为F= .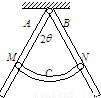
【答案】分析:通过A杆在竖直方向和水平方向平衡,结合对A杆力矩平衡,AB整体受力平衡求出弯杆C对杆A的作用力的方向和大小.
解答:解:因为AB是对称的,所以只分析A和C的受力.
设A上铰支座对杆A的水平支座反力为Rx,竖直反力为Ry(就是支座对杆的力) 杆C对A的作用力水平为Nx,竖直为Ny,则有:
(1)水平方向力平衡:Nx=Rx
(2)竖直力平衡:Ry+mg=Ny
(3)力矩平衡(A定点为力矩中心):mg× Lsinθ=Nx×
Lsinθ=Nx×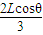 +Ny×
+Ny×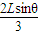
同时,对AB的整体来说,有:
(4)2Ry=2mg
联立以上4个方程,解得:Rx=1.5mgtanθ,Ry=mg(方向向上),Nx=1.5mgtanθ,Ny=0.
所以弯杆C对杆A的作用力的方向水平向左,大小为1.5mgtanθ.
故答案为:水平向左,1.5mgtanθ
点评:本题考查了受力平衡,力矩平衡,对学生的能力要求较高,难度较大.
解答:解:因为AB是对称的,所以只分析A和C的受力.
设A上铰支座对杆A的水平支座反力为Rx,竖直反力为Ry(就是支座对杆的力) 杆C对A的作用力水平为Nx,竖直为Ny,则有:
(1)水平方向力平衡:Nx=Rx
(2)竖直力平衡:Ry+mg=Ny
(3)力矩平衡(A定点为力矩中心):mg×
 Lsinθ=Nx×
Lsinθ=Nx×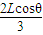 +Ny×
+Ny×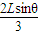
同时,对AB的整体来说,有:
(4)2Ry=2mg
联立以上4个方程,解得:Rx=1.5mgtanθ,Ry=mg(方向向上),Nx=1.5mgtanθ,Ny=0.
所以弯杆C对杆A的作用力的方向水平向左,大小为1.5mgtanθ.
故答案为:水平向左,1.5mgtanθ
点评:本题考查了受力平衡,力矩平衡,对学生的能力要求较高,难度较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如图所示,有两根长均为L、质量均为m的细导体棒a、b,其中a被水平放置在倾角为45°的绝缘光滑斜面上,b被水平固定在斜面的右侧,且与a在同一水平面上,a、b相互平行。当两细棒中均通以大小为I的同向电流时,a恰能在斜面上保持静止,关于b的电流在a处产生的磁场的磁感应强度B,下列说法正确的是
| A.方向竖直向上 |
B.大小为 |
C.大小为 |
| D.若使b竖直向下移动,a仍能保持静止 |
 长均为L、质量均为m的两根均匀直杆A、B,它们的上端用光滑铰链铰接,悬挂于天花板上,在距离两杆下端点均为L/3处,用光滑铰链M、N与弯杆C铰接,A、B两杆被弯杆C撑开的角度为2θ,弯杆C和铰链的质量均不计,则可知弯杆对杆A的作用力方向为
长均为L、质量均为m的两根均匀直杆A、B,它们的上端用光滑铰链铰接,悬挂于天花板上,在距离两杆下端点均为L/3处,用光滑铰链M、N与弯杆C铰接,A、B两杆被弯杆C撑开的角度为2θ,弯杆C和铰链的质量均不计,则可知弯杆对杆A的作用力方向为 长均为L,质量均为m的两根均匀直杆A,B,它们的上端用光滑铰链铰接,悬挂于天花板上,在距离两杆下端点均为
长均为L,质量均为m的两根均匀直杆A,B,它们的上端用光滑铰链铰接,悬挂于天花板上,在距离两杆下端点均为 如图所示,有两根长均为L、质量均为m的细导体棒a、b,其中a被水平放置在倾角为45°的绝缘光滑斜面上,b被水平固定在斜面的右侧,且与a在同一水平面上,a、b相互平行.当两细棒中均通以大小为I的同向电流时,a恰能在斜面上保持静止,关于b的电流在a处产生的磁场的磁感应强度B,下列说法正确的是( )
如图所示,有两根长均为L、质量均为m的细导体棒a、b,其中a被水平放置在倾角为45°的绝缘光滑斜面上,b被水平固定在斜面的右侧,且与a在同一水平面上,a、b相互平行.当两细棒中均通以大小为I的同向电流时,a恰能在斜面上保持静止,关于b的电流在a处产生的磁场的磁感应强度B,下列说法正确的是( )

