题目内容
13. 屋檐上每隔相同的时间间隔滴下一滴水,当第5滴正欲滴下时,第1滴已刚好到达地面,此时第3滴与第2滴分别位于高为1m的窗户的上、下沿,如图所示,问:
屋檐上每隔相同的时间间隔滴下一滴水,当第5滴正欲滴下时,第1滴已刚好到达地面,此时第3滴与第2滴分别位于高为1m的窗户的上、下沿,如图所示,问:(1)滴水的时间间隔是多少?
(2)第5滴与第4滴的间隔距离是多少?
(3)此屋檐离地面多高?
分析 (1)设滴水的时间间隔为T,知窗子的高度等于自由下落3T内的位移减去2T内的位移.根据自由落体运动的位移时间公式求出滴水的时间间隔;
(2)分别求出第三滴水和第四滴水下落的高度,进而求出高度差;
(3)通过滴水的时间间隔,可以知道一滴水下落到地面的时间,根据h=$\frac{1}{2}g{t}^{2}$求出屋檐离地面的高度.
解答 解,设相邻两滴水之间时间间隔为△t,第2滴、第3滴下落高度分别为h2、h3,则:${h}_{2}=\frac{1}{2}g(3△t)^{2}$ ${h}_{3}=\frac{1}{2}g(2△t)^{2}$
△h=h2-h3
联立各式,得:△t=0.2s
(2)由H=$\frac{1}{2}g{t}^{2}$得下落的距离为:H=0.2米
(3)高度为:${h}_{1}=\frac{1}{2}g(4△t)^{2}=\frac{1}{2}×10×0.{8}^{2}=3.2m$
答:(1)滴水的时间间隔是0.2s
(2)第5滴与第4滴的间隔距离是0.2m
(3)此屋檐离地面高为3.2m
点评 解决本题的关键知道自由落体运动是初速度为0,加速度为g的匀加速直线运动.本题也可以通过初速度为零的匀加速直线运动的推论,在相等时间间隔内的位移之比为1:3:5:7.求出下落的高度

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
4. 如图所示,一辆汽车从静止开始由甲地出发,沿平直公路开往乙地.汽车先做匀加速运动.接着做匀减速运动,开到乙地刚好停止.其速度图象如右图所示,那么在0~t0和t0~3t0两段时间内( )
如图所示,一辆汽车从静止开始由甲地出发,沿平直公路开往乙地.汽车先做匀加速运动.接着做匀减速运动,开到乙地刚好停止.其速度图象如右图所示,那么在0~t0和t0~3t0两段时间内( )
 如图所示,一辆汽车从静止开始由甲地出发,沿平直公路开往乙地.汽车先做匀加速运动.接着做匀减速运动,开到乙地刚好停止.其速度图象如右图所示,那么在0~t0和t0~3t0两段时间内( )
如图所示,一辆汽车从静止开始由甲地出发,沿平直公路开往乙地.汽车先做匀加速运动.接着做匀减速运动,开到乙地刚好停止.其速度图象如右图所示,那么在0~t0和t0~3t0两段时间内( )| A. | 平均速度大小之比为2:1 | B. | 平均速度大小之比为1:1 | ||
| C. | 位移大小之比为1:2 | D. | 加速度大小比为3:1 |
8. 如图是甲、乙两物体在同一直线上运动的s-t图象,以甲的出发点为原点,出发时间为计时起点,则( )
如图是甲、乙两物体在同一直线上运动的s-t图象,以甲的出发点为原点,出发时间为计时起点,则( )
 如图是甲、乙两物体在同一直线上运动的s-t图象,以甲的出发点为原点,出发时间为计时起点,则( )
如图是甲、乙两物体在同一直线上运动的s-t图象,以甲的出发点为原点,出发时间为计时起点,则( )| A. | 甲、乙同时出发 | |
| B. | 乙比甲先出发 | |
| C. | 甲出发时,乙在甲前边S0处 | |
| D. | 甲在途中停了一段时间,而乙没有停止 |
18.物体从离地面45m高处做自由落体运动(g取10m/s2),则下列选项中正确的是( )
| A. | 物体运动3 s后落地 | |
| B. | 物体落地时的速度大小为20 m/s | |
| C. | 物体在落地前最后1 s内的位移为25 m | |
| D. | 物体在整个下落过程中的平均速度为20 m/s |
5.下列关于电场强度的两个表达式E=$\frac{F}{q}$和E=$\frac{kQ}{{r}^{2}}$的叙述,正确的是( )
| A. | E=$\frac{F}{q}$是电场强度的定义式,F是放入电场中的电荷所受的力,q是产生电场的电荷的电荷量 | |
| B. | E=$\frac{F}{q}$是电场强度的计算式,F是放入电场中的电荷受的力,q是放入电场中电荷的电荷量,它适用于任何电场 | |
| C. | E=$\frac{kQ}{{r}^{2}}$是点电荷场强的定义式,Q是产生电场的电荷的电荷量,它不适用于匀强电场 | |
| D. | 从点电荷场强计算式分析库仑定律的表达式F=k$\frac{{q}_{1}{q}_{2}}{{r}^{2}}$,式$\frac{k{q}_{2}}{{r}^{2}}$是点电荷q2产生的电场在点电荷q1处的场强大小,而$\frac{k{q}_{1}}{{r}^{2}}$是点电荷q1产生的电场在点电荷q2处的场强的大小 |
2.一辆动电车做直线运动,速度随时间变化的函数关系为v=bt,其中b=0.3m/s2时( )
| A. | 电动车做匀速直线运动 | B. | 电动车做匀变速直线运动 | ||
| C. | 电动车初速度为0 | D. | 电动车的速度变化量是0.3 m/s |
8.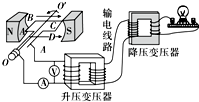 如图所示,匝数n=100匝、面积为S=0.448m2的导线框ABCD所在处的磁感应强度大小B=$\frac{\sqrt{2}}{10π}$ T.线框绕垂直于磁场的轴OO′以角速度ω=100π rad/s匀速转动,并与理想升压变压器相连进行远距离输电,升压变压器的原副线圈匝数比为2:5,理想降压变压器副线圈接入一只“220V 1100W”的灯泡,且灯泡正常发光,输电线路总电阻r=20Ω,输电线上损失的功率.导线框及其余导线电阻不计,电表均为理想电表.则下列说法中正确的是( )
如图所示,匝数n=100匝、面积为S=0.448m2的导线框ABCD所在处的磁感应强度大小B=$\frac{\sqrt{2}}{10π}$ T.线框绕垂直于磁场的轴OO′以角速度ω=100π rad/s匀速转动,并与理想升压变压器相连进行远距离输电,升压变压器的原副线圈匝数比为2:5,理想降压变压器副线圈接入一只“220V 1100W”的灯泡,且灯泡正常发光,输电线路总电阻r=20Ω,输电线上损失的功率.导线框及其余导线电阻不计,电表均为理想电表.则下列说法中正确的是( )
 如图所示,匝数n=100匝、面积为S=0.448m2的导线框ABCD所在处的磁感应强度大小B=$\frac{\sqrt{2}}{10π}$ T.线框绕垂直于磁场的轴OO′以角速度ω=100π rad/s匀速转动,并与理想升压变压器相连进行远距离输电,升压变压器的原副线圈匝数比为2:5,理想降压变压器副线圈接入一只“220V 1100W”的灯泡,且灯泡正常发光,输电线路总电阻r=20Ω,输电线上损失的功率.导线框及其余导线电阻不计,电表均为理想电表.则下列说法中正确的是( )
如图所示,匝数n=100匝、面积为S=0.448m2的导线框ABCD所在处的磁感应强度大小B=$\frac{\sqrt{2}}{10π}$ T.线框绕垂直于磁场的轴OO′以角速度ω=100π rad/s匀速转动,并与理想升压变压器相连进行远距离输电,升压变压器的原副线圈匝数比为2:5,理想降压变压器副线圈接入一只“220V 1100W”的灯泡,且灯泡正常发光,输电线路总电阻r=20Ω,输电线上损失的功率.导线框及其余导线电阻不计,电表均为理想电表.则下列说法中正确的是( )| A. | 输电线路的电流为0.98A | |
| B. | 电流表的读数为2.5A | |
| C. | 降压变压器的原副线圈匝数比为5:2 | |
| D. | 线圈从图示位置转过$\frac{π}{2}$的过程中,感应电动势的平均值和有效值之比为$\frac{2\sqrt{2}}{π}$ |
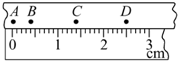 打点计时器每隔0.02 s打一次点,某次实验中得到的一条纸带,用毫米刻度尺测量情况如图所示,纸带在A、C间的平均速度为0.35 m/s,在A、D间的平均速度为0.42m/s,B点的瞬时速度更接近于0.35m/s.(结果保留两位有效数字)
打点计时器每隔0.02 s打一次点,某次实验中得到的一条纸带,用毫米刻度尺测量情况如图所示,纸带在A、C间的平均速度为0.35 m/s,在A、D间的平均速度为0.42m/s,B点的瞬时速度更接近于0.35m/s.(结果保留两位有效数字)