题目内容

在光滑绝缘的水平桌面上，有两个质量均为，电量为的完全相同的带电粒子P1和P2，在小孔A处以初速度为零先后释放．在平行板间距为的匀强电场中加速后，P1从C处对着圆心进入半径为R的固定圆筒中(筒壁上的小孔C只能容一个粒子通过)，圆筒内有垂直水平面向上的磁感应强度为B的匀强磁场．P1每次与筒壁发生碰撞均无电荷迁移，P1进入磁场第一次与筒壁碰撞点为D，，如图所示．延后释放的P2，将第一次欲逃逸出圆筒的P1正碰圆筒内，此次碰撞刚结束，立即改变平行板间的电压，并利用P2与P1之后的碰撞，将限制在圆筒内运动．碰撞过程均无机械能损失．设，求：在P2和P1相邻两次碰撞时间间隔内，粒子P1与筒壁的可能碰撞次数．

附：部分三角函数值

答案：
解析：

设开始加速电压为U1，P1、P2第一次碰撞后电压变为U2

设粒子在圆筒中与筒壁碰撞(n-1)次，转了K圈后从C点射出，运动时间为t1

P2在电场中运动时间为t2，欲使P1不逃逸出磁场有：

P1、P2碰撞后速度发生交换

欲使P2与P1碰撞后不穿出A点，与P1碰撞后P2返回距离为S，

通过讨论：只有当K=1，n=3，4，5，6，7，8时，不等式成立．

所以，粒子与圆筒碰撞的可能次数为2，3，4，5，6，7


练习册系列答案
相关题目
如图10所示，在光滑绝缘的水平桌面上有四个小球，带电量分别为-q、Q、-q、Q．四个小球构成一个菱形，-q、-q的连线与-q、Q的连线之间的夹角为α．若此系统处于平衡状态，则正确的关系式可能是（　　）
如图甲所示，在光滑绝缘的水平桌面上建立一xoy坐标系，平面处在周期性变化的电场和磁场中，电场和磁场的变化规律如图乙所示（规定沿+y方向为电场强度的正方向，竖直向下为磁感应强度的正方向）．在t=0时刻，一质量为10g、电荷量为0.1C的带电金属小球自坐标原点O处，以v0=2m/s的速度沿x轴正方向射出．已知E0=0.2N/C、B0=0.2πT．求：
（1）t=1s末速度的大小和方向；
（2）1s～2s内，金属小球在磁场中做圆周运动的半径和周期；
（3）在给定的坐标系中，大体画出小球在0到6S内运动的轨迹示意图．
（4）6s内金属小球运动至离x轴最远点的位置坐标．
如图甲所示，在光滑绝缘的水平桌面上建立一xoy坐标系，平面处在周期性变化的电场和磁场中，电场和磁场的变化规律如图乙所示（规定沿+y方向为电场强度的正方向，竖直向下为磁感应强度的正方向）．在t=0时刻，一质量为10g、电荷量为0.1C的带电金属小球自坐标原点O处，以v0=2m/s的速度沿x轴正方向射出．已知E0=0.2N/C、B0=0.2πT．求：
（1）t=1s末速度的大小和方向；
（2）1s～2s内，金属小球在磁场中做圆周运动的半径和周期；
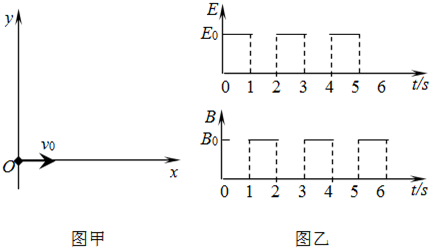
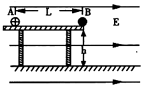（3）（2n-1）s～2ns（n=1，2，3，…）内金属小球运动至离x轴最远点的位置坐标．精英家教网
精英家教网如图所示，在光滑绝缘的水平桌面上有两个静止的质量均为m=0.2kg的小球A和B，B在桌面边缘，A和B均可视为质点，A球所带的电荷量 q=+0.1C，B球是绝缘体，不带电，桌面离水平地面的高h=0.05m．开始时A、B两小球相距L=0.1m，然后，在整个空间中加上水平向右、大小E=1O N/C的匀强电场，在电场力的作用下，A开始向右运动，并与B球发生正碰，碰撞过程中A、B的总动能无损失，A和B之间无电荷转移（重力加速度g=1Om/s2）．求：
（1）在小球A与B相碰前A的速率为多少？
（2）A、B两小球的落地点之间的距离是多大？
精英家教网如图所示，在光滑绝缘的水平桌面上方固定着电荷量大小相等的两个点电荷q1、q2，一个带电小球（可视为点电荷）恰好围绕O点在桌面上做匀速圆周运动．已知O、q1、q2在同一竖直线上，下列判断正确的是（　　）
A、圆轨道上的电势处处相等B、圆轨道上的电场强度处处相等C、点电荷q1对小球的库仑力是吸引力D、q1、q2可能为异种电荷

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网