题目内容
6. 如图,水平桌面距地面足够高,质量为m长度为a的匀质细链条有$\frac{1}{4}$部分悬于桌边,将链条由静止释放,当链条刚离开桌面时,链条的速率为多大?(不计一切摩擦及空气阻力)
如图,水平桌面距地面足够高,质量为m长度为a的匀质细链条有$\frac{1}{4}$部分悬于桌边,将链条由静止释放,当链条刚离开桌面时,链条的速率为多大?(不计一切摩擦及空气阻力)
分析 在链条运动的过程中,对整个系统而言,机械能守恒.抓住系统重力势能的减小量等于动能的增加量,求出链条刚离开桌面时的速率.
解答 解:取桌面为零势能面,开始时链条的重力势能为:E1=-$\frac{1}{4}$mg•$\frac{1}{8}$a
当链条刚脱离桌面时的重力势能:E2=-mg•$\frac{a}{2}$
故重力势能的变化量:△E=E2-E1=-$\frac{1}{4}$mg•$\frac{1}{8}$a-(-mg•$\frac{a}{2}$)=$\frac{15}{32}$mga
根据机械能守恒得:△E=$\frac{1}{2}m{v}^{2}$
联立解得:v=$\frac{{\sqrt{15ga}}}{4}$
答:当链条刚离开桌面时,链条的速率为$\frac{{\sqrt{15ga}}}{4}$.
点评 本题解题时,要明确零势能面的选取是任意的,也可以选链条滑至刚刚离开桌边时链条的中心为零势能面,要注意重力势能的正负.

练习册系列答案
相关题目
17.如图所示,矩形线圈abcd由静止开始运动,若要使线圈中产生感应电流,则线圈的运动情况应该是( )


| A. | 向右平动(ad边还没有进入磁场) | B. | 向上平动(ab边还没有离开磁场) | ||
| C. | 以bc边为轴转动(ad边还未转入磁场) | D. | 平行于磁场向外平动 |
1. 将横截面积为S的玻璃管弯成如图所示的连通器,放在水平桌面上,左、右管处在竖直状态,先关闭阀门K,往左、右管中分别注入高度为h1和h2、密度为ρ的液体,然后打开阀门K,直到液体静止.在上述过程中,重力对液体做的功为( )
将横截面积为S的玻璃管弯成如图所示的连通器,放在水平桌面上,左、右管处在竖直状态,先关闭阀门K,往左、右管中分别注入高度为h1和h2、密度为ρ的液体,然后打开阀门K,直到液体静止.在上述过程中,重力对液体做的功为( )
 将横截面积为S的玻璃管弯成如图所示的连通器,放在水平桌面上,左、右管处在竖直状态,先关闭阀门K,往左、右管中分别注入高度为h1和h2、密度为ρ的液体,然后打开阀门K,直到液体静止.在上述过程中,重力对液体做的功为( )
将横截面积为S的玻璃管弯成如图所示的连通器,放在水平桌面上,左、右管处在竖直状态,先关闭阀门K,往左、右管中分别注入高度为h1和h2、密度为ρ的液体,然后打开阀门K,直到液体静止.在上述过程中,重力对液体做的功为( )| A. | $\frac{1}{4}$ρgS(h1-h2)2 | B. | $\frac{1}{2}$ρgS(h1-h2)2 | C. | ρgS(h1-h2) | D. | $\frac{1}{4}$ρgS(h1-h2) |
11.关于功率,以下说法不正确的是( )
| A. | 单位时间内物体做功越多,其功率越大 | |
| B. | 物体做功越多,它的功率就越大 | |
| C. | 物体做功越快,它的功率就越大 | |
| D. | 额定功率是发动机正常工作时的最大输出功率 |
15. 如图所示,在光滑的水平面上,质量为m1的小球A以速率v0向右运动.在小球的前方O点处有一质量为m2的小球B处于静止状态,Q点处为一竖直的墙壁.小球A与小球B发生弹性碰撞后两小球均向右运动,小球B与墙壁碰撞后原速率返回并与小球A在P点相遇,$\overline{PQ}$=2$\overline{PO}$,则两小球质量之比m1:m2为( )
如图所示,在光滑的水平面上,质量为m1的小球A以速率v0向右运动.在小球的前方O点处有一质量为m2的小球B处于静止状态,Q点处为一竖直的墙壁.小球A与小球B发生弹性碰撞后两小球均向右运动,小球B与墙壁碰撞后原速率返回并与小球A在P点相遇,$\overline{PQ}$=2$\overline{PO}$,则两小球质量之比m1:m2为( )
 如图所示,在光滑的水平面上,质量为m1的小球A以速率v0向右运动.在小球的前方O点处有一质量为m2的小球B处于静止状态,Q点处为一竖直的墙壁.小球A与小球B发生弹性碰撞后两小球均向右运动,小球B与墙壁碰撞后原速率返回并与小球A在P点相遇,$\overline{PQ}$=2$\overline{PO}$,则两小球质量之比m1:m2为( )
如图所示,在光滑的水平面上,质量为m1的小球A以速率v0向右运动.在小球的前方O点处有一质量为m2的小球B处于静止状态,Q点处为一竖直的墙壁.小球A与小球B发生弹性碰撞后两小球均向右运动,小球B与墙壁碰撞后原速率返回并与小球A在P点相遇,$\overline{PQ}$=2$\overline{PO}$,则两小球质量之比m1:m2为( )| A. | 7:5 | B. | 4:3 | C. | 2:1 | D. | 5:3 |
16.如图1一矩形线圈,绕垂直于匀强磁场并位于线圈平面的固定轴转动,线圈中的感应电动势e随时间t的变化如图2,下列说法中正确的是( )
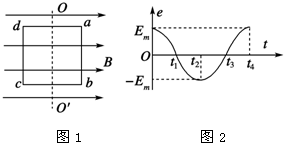

| A. | t1时刻通过线圈的磁通量为零 | |
| B. | t2时刻线圈位于中性面 | |
| C. | t3时刻通过线圈的磁通量变化率的绝对值最大 | |
| D. | 每当e变化方向时,通过线圈的磁通量最大 |
 如图,一台理想变压器,原线圈2200匝,副线圈440匝,并接一个100Ω的负载电阻若把原线圈接在220V交流电源上,则电压表示数为44V,电流表示数为0.44A.如果接上110V的直流电源,则电压表的读数为0V.
如图,一台理想变压器,原线圈2200匝,副线圈440匝,并接一个100Ω的负载电阻若把原线圈接在220V交流电源上,则电压表示数为44V,电流表示数为0.44A.如果接上110V的直流电源,则电压表的读数为0V. 如图所示,一物块在水平恒力F=6N的作用下从A点由静止开始沿水平直轨道运动到B点,物块飞出后越过“壕沟”落在平台EG段,已知物块的质量m=1kg,物块与水平直轨道间的动摩擦因数为μ=0.4,AB段长L=9m,BE的高度差h=0.8m,BE的水平距离x=1.6m,若物块可看做质点,空气阻力不计,g取10m/s2.求:
如图所示,一物块在水平恒力F=6N的作用下从A点由静止开始沿水平直轨道运动到B点,物块飞出后越过“壕沟”落在平台EG段,已知物块的质量m=1kg,物块与水平直轨道间的动摩擦因数为μ=0.4,AB段长L=9m,BE的高度差h=0.8m,BE的水平距离x=1.6m,若物块可看做质点,空气阻力不计,g取10m/s2.求: