题目内容
 如图所示,质量0.2Kg的物体沿h=0.8m的弧形轨道由静止开始下滑,到达底端离开轨道瞬间速度方向与水平方向成30°角,速度大小为3m/s,在这一过程中,根据本题的条件下面那些物理量可求出来(g取10m/s2)( )
如图所示,质量0.2Kg的物体沿h=0.8m的弧形轨道由静止开始下滑,到达底端离开轨道瞬间速度方向与水平方向成30°角,速度大小为3m/s,在这一过程中,根据本题的条件下面那些物理量可求出来(g取10m/s2)( )分析:根据动能定理求出物体克服阻力做功的大小,结合末速度的大小和方向,根据P=mgvcosα求出重力的瞬时功率.
解答:解:A、物体做曲线运动,无法求出物体的合力以及下滑的时间.故A、B错误.
C、根据动能定理得,mgh-Wf=
mv2-0,则克服阻力做功大小Wf=mgh-
mv2=0.2×10×0.8-
×0.2×9J=0.7J.故C正确.
D、重力的瞬时功率P=mgvcosα=0.2×10×3cos60°W=3W.故D正确.
故选:CD.
C、根据动能定理得,mgh-Wf=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
D、重力的瞬时功率P=mgvcosα=0.2×10×3cos60°W=3W.故D正确.
故选:CD.
点评:本题考查了动能定理以及瞬时功率的基本运用,求解瞬时功率时注意力与速度方向的夹角.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示,质量M=2.0kg的小车放在光滑水平面上,在小车右端放一质量m=1.0kg的滑块A,滑块与小车之间动摩擦因数μ=0.5.当滑块与小车同时分别受到水平向左F1=6.0N的拉力和水平向右F2=9.0N的拉力后开始运动,经0.4s后同时撤去两水平力,设滑块一直未从小车上滑下,(取g=10m/s2)
如图所示,质量M=2.0kg的小车放在光滑水平面上,在小车右端放一质量m=1.0kg的滑块A,滑块与小车之间动摩擦因数μ=0.5.当滑块与小车同时分别受到水平向左F1=6.0N的拉力和水平向右F2=9.0N的拉力后开始运动,经0.4s后同时撤去两水平力,设滑块一直未从小车上滑下,(取g=10m/s2)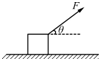 如图所示,质量m=2.0kg的木块静止在水平面上,用大小F=20N、方向与水平方向成θ=37°角的力拉动木块,当木块运动到x=10m力F.不计空气阻力.已知木块与水平面间的动摩擦因数?=0.2,sin37°=0.6,cos37°=0.8.g取10m/s2.求:
如图所示,质量m=2.0kg的木块静止在水平面上,用大小F=20N、方向与水平方向成θ=37°角的力拉动木块,当木块运动到x=10m力F.不计空气阻力.已知木块与水平面间的动摩擦因数?=0.2,sin37°=0.6,cos37°=0.8.g取10m/s2.求: 如图所示,质量m=2.0kg的物体在水平外力的作用下在水平面上运动,物体和水平面间的动摩擦因数μ=0.05,已知物体运动过程中的坐标与时间的关系为
如图所示,质量m=2.0kg的物体在水平外力的作用下在水平面上运动,物体和水平面间的动摩擦因数μ=0.05,已知物体运动过程中的坐标与时间的关系为 如图所示,质量0.1kg的小球.从光滑轨道顶端滚下,圆轨道半径R=0.5m.小球经过A和B时,速度分别为VA=4m/s和VB=8m/s.设g=10m/s2
如图所示,质量0.1kg的小球.从光滑轨道顶端滚下,圆轨道半径R=0.5m.小球经过A和B时,速度分别为VA=4m/s和VB=8m/s.设g=10m/s2 如图所示,质量为2.0×103kg的汽车在水平公路上行驶,当汽车经过半径为60m的弯路时,车速为20m/s.此时汽车转弯所需要的向心力大小为
如图所示,质量为2.0×103kg的汽车在水平公路上行驶,当汽车经过半径为60m的弯路时,车速为20m/s.此时汽车转弯所需要的向心力大小为