题目内容
2. 如图所示,质量为2kg的物体A静止在竖直的轻弹簧上面,若将一个质量为3kg的物体B轻轻放在A上,刚刚放上瞬间,B对A的压力大小为(取g=10m/s2)( )
如图所示,质量为2kg的物体A静止在竖直的轻弹簧上面,若将一个质量为3kg的物体B轻轻放在A上,刚刚放上瞬间,B对A的压力大小为(取g=10m/s2)( )| A. | 30N | B. | 0N | C. | 18N | D. | 12N |
分析 放上B的瞬间,先对整体研究,根据牛顿第二定律求出加速度,再隔离分析,根据牛顿第二定律求出A对B的支持力的大小.
解答 解:开始弹簧的弹力等于A的重力,即F=mAg放上B的瞬间,弹簧弹力不变,对整体分析,根据牛顿第二定律得:
a=$\frac{({m}_{A}+{m}_{B\;})g-F\;}{{m}_{A\;}+{m}_{B\;}}$=$\frac{{m}_{B\;}g\;}{{m}_{A\;}+{m}_{B\;}}=\frac{3×10}{2+3}m/{s}^{2}=6m/{s}^{2}$.
隔离对B分析,有:mBg-N=mBa,
则:N=mB(g-a)=3×(10-6)N=12N.故D正确,A、B、C错误.
故选:D.
点评 解决本题的关键能够正确地受力分析,运用牛顿第二定律进行求解,掌握整体法和隔离法的运用.

练习册系列答案
相关题目
12.起重机用钢绳将重物竖直向上匀速提升,在重物匀速上升的过程中( )
| A. | 重物的重力势能逐渐增大 | B. | 钢绳对重物的拉力逐渐增大 | ||
| C. | 钢绳对重物的拉力的功率逐渐增大 | D. | 重物的动能逐渐增大 |
10.如图是氧气分子在不同温度(0℃和100℃)下的速率分布,由图可得信息( )


| A. | 同一温度下,氧气分子呈现出“中间多,两头少”的分布规律 | |
| B. | 随着温度的升高,每一个氧气分子的速率都增大 | |
| C. | 随着温度的升高,氧气分子的平均速率变小 | |
| D. | 随着温度的升高,氧气分子中速率小的分子所占的比例高 |
7. 如图所示,质量为m的物体以速度v0离开桌面后经过A点时,所具有的机械能是(以桌面为零势能面,不计空气阻力)( )
如图所示,质量为m的物体以速度v0离开桌面后经过A点时,所具有的机械能是(以桌面为零势能面,不计空气阻力)( )
 如图所示,质量为m的物体以速度v0离开桌面后经过A点时,所具有的机械能是(以桌面为零势能面,不计空气阻力)( )
如图所示,质量为m的物体以速度v0离开桌面后经过A点时,所具有的机械能是(以桌面为零势能面,不计空气阻力)( )| A. | $\frac{1}{2}$mv02 | B. | $\frac{1}{2}$mv02+mgh | C. | $\frac{1}{2}$mv02-mgh | D. | $\frac{1}{2}$mv02+mg(H-h) |
11.科学家发现太阳系有一个天体,天体的运行轨道近似地看作圆,天体的半径为R、质量为m,天体与太阳的中心间距为r,若万有引力常量为G,太阳的质量为M,该天体运行的公转周期为( )
| A. | 2π$\sqrt{\frac{{r}^{3}}{Gm}}$ | B. | 2π$\sqrt{\frac{{r}^{3}}{GM}}$ | C. | 2π$\sqrt{\frac{{R}^{3}}{GM}}$ | D. | 2π$\sqrt{\frac{{R}^{3}}{Gm}}$ |
 如图,带电量为+q、质量为m的粒子(不计重力)由静止开始经A、B间电场加速后,沿中心线匀速射入带电金属板C、D间后粒子水平射入,已知C、D间电压为U0,板间距离为d,C、D间有垂直于纸面向里的匀强磁场,磁感应强度分别为B0.
如图,带电量为+q、质量为m的粒子(不计重力)由静止开始经A、B间电场加速后,沿中心线匀速射入带电金属板C、D间后粒子水平射入,已知C、D间电压为U0,板间距离为d,C、D间有垂直于纸面向里的匀强磁场,磁感应强度分别为B0.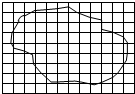 某同学在实验室做“用油膜法估测分子直径的大小”实验中,已知油酸酒精溶液的浓度为每104mL溶液中有纯油酸6mL.用注射器抽得上述溶液2mL,现缓慢地滴出1mL溶液,共有液滴数为50滴.把1滴该溶液滴入盛水的浅盘上,在刻有小正方形坐标的玻璃板上描出油膜的轮廓(如图所示),坐标中小正方形方格的边长为20mm.试问:
某同学在实验室做“用油膜法估测分子直径的大小”实验中,已知油酸酒精溶液的浓度为每104mL溶液中有纯油酸6mL.用注射器抽得上述溶液2mL,现缓慢地滴出1mL溶液,共有液滴数为50滴.把1滴该溶液滴入盛水的浅盘上,在刻有小正方形坐标的玻璃板上描出油膜的轮廓(如图所示),坐标中小正方形方格的边长为20mm.试问: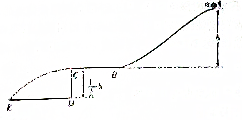 如图所示,a球从距BC高h的A处静止释放后,沿光滑轨道ABC下滑,在C处水平抛出.已知C离水平地面的高度为$\frac{1}{2}$h,重力加速度为g,求:
如图所示,a球从距BC高h的A处静止释放后,沿光滑轨道ABC下滑,在C处水平抛出.已知C离水平地面的高度为$\frac{1}{2}$h,重力加速度为g,求: