题目内容
9. 如图所示,在游乐节目中,一质量m=50kg的选手抓住竖直绳下端的抓手以v0=5m/s的水平速度开始摆动,当摆到与竖直方向夹角θ=37°时,选手松手,松手后的上升过程中选手水平速度保持不变,运动到水平传送带左端A时速度刚好水平,并在传动带上滑行,传送带以v=2.8m/s的速度向右匀速运动.已知绳子的悬挂点到抓手的距离L=6m,传送带两端点A、B间的距离s=3.7m,选手与传送带的动摩擦因数μ=0.4,若把选手看成质点,且不考虑空气阻力和绳的质量.g=10m/s2,sin37°=0.6,cos37°=0.8,求:
如图所示,在游乐节目中,一质量m=50kg的选手抓住竖直绳下端的抓手以v0=5m/s的水平速度开始摆动,当摆到与竖直方向夹角θ=37°时,选手松手,松手后的上升过程中选手水平速度保持不变,运动到水平传送带左端A时速度刚好水平,并在传动带上滑行,传送带以v=2.8m/s的速度向右匀速运动.已知绳子的悬挂点到抓手的距离L=6m,传送带两端点A、B间的距离s=3.7m,选手与传送带的动摩擦因数μ=0.4,若把选手看成质点,且不考虑空气阻力和绳的质量.g=10m/s2,sin37°=0.6,cos37°=0.8,求:(1)选手放开抓手时的速度大小及选手在传送带上从A运动到B的时间;
(2)选手在传送带上运动时传送带的发动机需要多输出的能量.
分析 (1)选手拉着绳子在摆动的过程中机械能守恒,根据机械能守恒定律求出选手放开绳子时的速度大小;根据平行四边形定则求出选手放开绳子时水平方向和竖直方向上的分速度,当选手到达最高点时,竖直方向上的分速度为零,选手在传送带上的初速度等于水平分速度,结合牛顿第二定律和运动学公式求出选手在传送带上滑行时间;
(2)求出选手相对于传送带的路程,根据Q=f△x求出摩擦而产生的热量,电动机多输出的能量等于物体增加的动能与热量之和.
解答 解:(1)由机械能守恒定律得:
$\frac{1}{2}m{v}_{0}^{2}$=mgL (1-cos37°)+$\frac{1}{2}m{v}^{2}$
代入数据解得:v2=1m/s.
选手在放开绳子时,水平速度为vx,竖直速度为vy,则有:vx=vcos37°=1×0.8=0.8m/s.
选手在最高点站到传送带上A点有0.8m/s向右的速度,在传送带上做匀减速直线运动.
选手的加速度大小为:a=μg=0.4×10=4m/s2.
减速到跟传送带具有相同速度时所需时间为:
v=vx+at1
t1=$\frac{2-4}{-4}$=0.5s
x1=$\frac{v+{v}_{2}}{2}$t1=$\frac{0.8+2.8}{2}$×0.5=0.9m
△x=x-x1=3.7-0.9=2.8m
在△x内做匀速运动所需时间为:
t2=$\frac{△x}{△t}$=$\frac{2.8}{2.8}$=1s
故所需时间为:t=t1+t2=1+0.5s=1.5s;
(2)选手增加的动能为:
EK=$\frac{1}{2}$mv2-$\frac{1}{2}$mvx2=$\frac{1}{2}$×50×(2.82-0.82)=180J;
摩擦力做功转化为内能为:Q=μmg(vt1-x1)=0.4×50×10×(2.8×0.5-0.9)=100J;
发动机需要多输出的能量为:E=180+100=280J;
答:(1)选手放开绳子时的速度大小为1m/s;选手在传送带上从A运动到B的时间为1.5s;
(2)选手在传送带上时传送带的发动机需要多输出的能量为280J.
点评 本题综合考查了机械能守恒定律、牛顿第二定律和运动学公式以及功能关系,综合性较强,对学生的能力要求较高,是一道好题.

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案| A. | “爆胎”前随着温度升高,车胎内气体压强将增大 | |
| B. | “爆胎”前随着温度升高,车胎内气体将向外放出热量 | |
| C. | “爆胎”是车胎所有气体分子的动能都急剧增大造成的 | |
| D. | “爆胎”是车胎内气体分子间斥力急剧增大造成的 |
| A. | 一个气体分子的体积等于气体的摩尔体积与阿伏加德罗常数之比 | |
| B. | 分子间相互作用的引力和斥力一定随分子间的距离增大而减小 | |
| C. | 气体分子热运动的平均动能减小,气体的压强一定减小 | |
| D. | 分子势能随分子间距离的增大可能增大、也可能减少 |



 如图所示,M、N为两块带等量异种电荷的平行金属板,两板间电压可取从零到某一最大值之间的各种数值.静止的带电粒子带电荷量为+q,质量为m(不计重力),从点P经电场加速后,从小孔Q进入N板右侧的匀强磁场区域,磁感应强度大小为B,方向垂直于纸面向外,CD为磁场边界上的一绝缘板,它与N板的夹角为θ=45°,孔Q到板的下端C的距离L,当M、N两板间电压取最大值时,粒子恰垂直打在CD板上,求:
如图所示,M、N为两块带等量异种电荷的平行金属板,两板间电压可取从零到某一最大值之间的各种数值.静止的带电粒子带电荷量为+q,质量为m(不计重力),从点P经电场加速后,从小孔Q进入N板右侧的匀强磁场区域,磁感应强度大小为B,方向垂直于纸面向外,CD为磁场边界上的一绝缘板,它与N板的夹角为θ=45°,孔Q到板的下端C的距离L,当M、N两板间电压取最大值时,粒子恰垂直打在CD板上,求: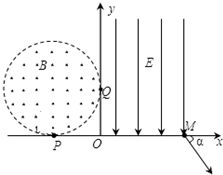 如图所示,在直角坐标系xOy平面的第Ⅱ象限内有半径为R的圆O1分别与x轴、y轴相切于P(-R,0)、Q(0,R) 两点,圆O1内存在垂直于xOy平面向外的匀强磁场,磁感应强度为B.与y轴负方向平行的匀强电场左边界与y轴重合,右边界交x轴于M点,一带正电的粒子A(重力不计)电荷量为q、质量为m,以某一速率垂直于x轴从P点射入磁场,经磁场偏转恰好从Q点进入电场,最后从M点以与x轴正向夹角为45°的方向射出电场.求:
如图所示,在直角坐标系xOy平面的第Ⅱ象限内有半径为R的圆O1分别与x轴、y轴相切于P(-R,0)、Q(0,R) 两点,圆O1内存在垂直于xOy平面向外的匀强磁场,磁感应强度为B.与y轴负方向平行的匀强电场左边界与y轴重合,右边界交x轴于M点,一带正电的粒子A(重力不计)电荷量为q、质量为m,以某一速率垂直于x轴从P点射入磁场,经磁场偏转恰好从Q点进入电场,最后从M点以与x轴正向夹角为45°的方向射出电场.求: