题目内容
（B类题）如图（1）所示，光滑水平面上有A、B两物块，已知A物块的质量mA=1kg．初始时刻B静止，A以一定的初速度向右运动，之后与B发生碰撞并一起运动，它们的位移-时间图象如图（2）所示（规定向右为位移的正方向）．因为系统所受的合外力 ，所以动量守恒，由此可以推算出B物块的质量mB kg．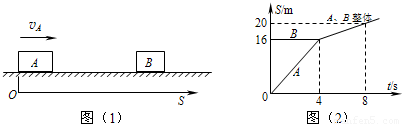
【答案】分析：知道动量守恒的条件．
从位移-时间图象中找出物体的速度．
根据动量守恒定律列出等式解决问题．
解答：解：因为系统所受的合外力等于零，所以系统动量守恒．
从位移-时间图象中知道：碰撞前A、B速度分别为4m/s，0．
碰撞后A、B速度为1m/s．
根据动量守恒定律列出等式：
mAvA+0=（mA+mB）v
解得：mB=3kg．
故答案为：等于零，3．
点评：应用动量守恒定律时要清楚研究的对象和守恒条件．
通过位移-时间图象得到一些信息．
从位移-时间图象中找出物体的速度．
根据动量守恒定律列出等式解决问题．
解答：解：因为系统所受的合外力等于零，所以系统动量守恒．
从位移-时间图象中知道：碰撞前A、B速度分别为4m/s，0．
碰撞后A、B速度为1m/s．
根据动量守恒定律列出等式：
mAvA+0=（mA+mB）v
解得：mB=3kg．
故答案为：等于零，3．
点评：应用动量守恒定律时要清楚研究的对象和守恒条件．
通过位移-时间图象得到一些信息．
练习册系列答案
相关题目
（2011?虹口区二模） （B类题）如图（1）所示，光滑水平面上有A、B两物块，已知A物块的质量mA=1kg．初始时刻B静止，A以一定的初速度向右运动，之后与B发生碰撞并一起运动，它们的位移-时间图象如图（2）所示（规定向右为位移的正方向）．因为系统所受的合外力
【A第三、四类学校的学校做此题】如图所示，粗糙水平轨道AB与竖直平面内的光滑轨道BC在B处平滑连接，B、C分别为半圆轨道的最低点和最高点．一个质量m的小物体P被一根细线拴住放在水平轨道上，细线的左端固定在竖直墙壁上．在墙壁和P之间夹一根被压缩的轻弹簧，此时P到B点的距离为x0．物体P与水平轨道间的动摩擦因数为μ，半圆轨道半径为R．现将细线剪断，P被弹簧向右弹出后滑上半圆轨道，经过C点时，对轨道的压力为重力的一半．求：
A类题(适合于使用一期课改教材的考生)
19A.某滑板爱好者在离地h＝1.8m高的平台上滑行，水平离开A点后落在水平地面的B点，其水平位移S1 ＝3m，着地时由于存在能量损失，着地后速度变为v＝4m／s，并以此为初速沿水平地面滑行S2 ＝8m后停止.已知人与滑板的总质量m＝60kg.求
(1)人与滑板在水平地面滑行时受到的平均阻力大小；
(2)人与滑板离开平台时的水平初速度.(空气阻力忽略不计，g=10m／s2)
B类题(适合于使用二期课改教材的考生)
19B.如图所示，某人乘雪橇从雪坡经A点滑至B点，接着沿水平路面滑至C点停止.人与雪橇的总质量为70kg.表中记录了沿坡滑下过程中的有关数据，请根据图表中的数据解决下列问题：
位置 | A | B | C |
速度(m/s) | 2.0 | 12.0 | 0 |
时刻(s) | 0 | 4 | 10 |
(1)人与雪橇从A到B的过程中，损失的机械能为多少?
(2)设人与雪橇在BC段所受阻力恒定，求阻力大小.
(g ＝10m／s2)
