题目内容
如图所示,将粗细相同的两段均匀棒A和B粘合在一起,并在粘合处用绳悬挂起来,棒恰好处于水平位置并保持平衡.如果A的密度是B的密度的2倍,则A与B的长度之比为 ,A与B的重力之比为 .
【答案】分析:先根据公式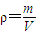 ,用两棒的长度表示两段棒的质量之比,再根据力矩平衡条件列式,求解A、B长度之比;由m=ρV得到质量之比,即可求得重力之比.
,用两棒的长度表示两段棒的质量之比,再根据力矩平衡条件列式,求解A、B长度之比;由m=ρV得到质量之比,即可求得重力之比.
解答:解:设A、B两棒的长度分别为LA、LB,质量分别为mA、mB,密度分别为ρA、ρB,两棒的横截面积为S.
则 mA:mB=ρALAS:ρBLBS
由题,ρA=2ρB,得 mA:mB=2LA:LB…①
根据力矩平衡条件得
mAg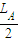 =mBg
=mBg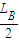 …②
…②
联立①②解得,LA:LB=1: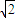
重力之比GA:GB=mA:mB=ρALAS:ρBLBS=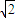 :1.
:1.
故答案为:1: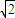 ,
,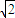 :1.
:1.
点评:本题关键要用长度表示质量关系,再根据力矩平衡条件进行求解.
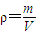 ,用两棒的长度表示两段棒的质量之比,再根据力矩平衡条件列式,求解A、B长度之比;由m=ρV得到质量之比,即可求得重力之比.
,用两棒的长度表示两段棒的质量之比,再根据力矩平衡条件列式,求解A、B长度之比;由m=ρV得到质量之比,即可求得重力之比.解答:解:设A、B两棒的长度分别为LA、LB,质量分别为mA、mB,密度分别为ρA、ρB,两棒的横截面积为S.
则 mA:mB=ρALAS:ρBLBS
由题,ρA=2ρB,得 mA:mB=2LA:LB…①
根据力矩平衡条件得
mAg
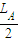 =mBg
=mBg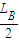 …②
…②联立①②解得,LA:LB=1:
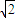
重力之比GA:GB=mA:mB=ρALAS:ρBLBS=
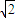 :1.
:1.故答案为:1:
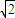 ,
,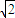 :1.
:1.点评:本题关键要用长度表示质量关系,再根据力矩平衡条件进行求解.

练习册系列答案
相关题目
 如图所示,将粗细相同的两段均匀棒A和B粘合在一起,并在粘合处用绳悬挂起来,棒恰好处于水平位置并保持平衡.如果A的密度是B的密度的2倍,则A与B的长度之比为
如图所示,将粗细相同的两段均匀棒A和B粘合在一起,并在粘合处用绳悬挂起来,棒恰好处于水平位置并保持平衡.如果A的密度是B的密度的2倍,则A与B的长度之比为

