题目内容
如图,半圆形凹槽的半径为R,O点为其圆心。在与O点等高的边缘A、B两点分别以速度v1、v2水平同时相向抛出两个小球,已知v1∶v2=1∶3,两小球恰落在弧面上的P点。则以下说法中正确的是(?? )

A.∠AOP为45°
B.若要使两小球落在P点右侧的弧面上同一点,则应使v1、v2都增大
C.改变v1、v2,只要两小球落在弧面上的同一点,v1与v2之和就不变
D.若只增大v1,两小球可在空中相遇
【答案】
D
【解析】
试题分析:A、连接OP,过P点作AB的垂线,垂足为D,如图所示:

两球在竖直方向运动的位移相等,所以运动时间相等,两球水平方向做运动直线运动,所以
而AD+BD=2R,所以 ,所以
,所以 ,所以cos∠AOP=
,所以cos∠AOP= 即∠AOP=60°,故A错误;
即∠AOP=60°,故A错误;
B、若要使两小球落在P点右侧的弧面上同一点,则A球水平方向位移增大,B球水平位移减小,而两球运动时间相等,所以应使v1增大,v2减小,故B错误;

C、要两小球落在弧面上的同一点,则水平位移之和为2R,则(v1+v2)t=2R,落点不同,竖直方向位移就不同,t也不同,所以v1+v2也不是一个定值,故C错误;
D、若只增大v1,而v2不变,则两球运动轨迹如图所示,由图可知,两球必定在空中相遇,故D正确.
故选D
考点:平抛运动的规律。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示是固定在光滑水平地面上的两条光滑长直导轨(俯视图).导轨内放置一个木质滑块A,滑块A的左半部是半径为R的半圆柱形光滑凹槽,木质滑块的宽度为2R.现有半径r(r<<R)的金属小球沿水平面以初速度v0冲向滑块,从滑块的一侧半圆形槽口边缘进入.已知金属小球的质量为m,木质滑块A的质量为3m,整个运动过程中无机械能损失.求:
如图所示是固定在光滑水平地面上的两条光滑长直导轨(俯视图).导轨内放置一个木质滑块A,滑块A的左半部是半径为R的半圆柱形光滑凹槽,木质滑块的宽度为2R.现有半径r(r<<R)的金属小球沿水平面以初速度v0冲向滑块,从滑块的一侧半圆形槽口边缘进入.已知金属小球的质量为m,木质滑块A的质量为3m,整个运动过程中无机械能损失.求: 如图所示是固定在水平地面上的横截面为“
如图所示是固定在水平地面上的横截面为“ ”形的光滑长直导轨槽,槽口向上(图为俯视图).槽内放置一个木质滑块,滑块的左半部是半径为R的半圆柱形光滑凹槽,木质滑块的宽度为2R,比“
”形的光滑长直导轨槽,槽口向上(图为俯视图).槽内放置一个木质滑块,滑块的左半部是半径为R的半圆柱形光滑凹槽,木质滑块的宽度为2R,比“ ”形槽的宽度略小.现有半径r(r<<R)的金属小球以水平初速度V0冲向滑块,从滑块的一侧半圆形槽口边缘进入.已知金属小球的质量为m,木质滑块的质量为3m,整个运动过程中无机械能损失.求:
”形槽的宽度略小.现有半径r(r<<R)的金属小球以水平初速度V0冲向滑块,从滑块的一侧半圆形槽口边缘进入.已知金属小球的质量为m,木质滑块的质量为3m,整个运动过程中无机械能损失.求: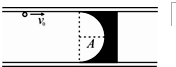 如图所示,固定在水平面上的横截面为“
如图所示,固定在水平面上的横截面为“ ”形的光滑长直导轨槽,槽口向上,槽内放置一金属滑块,滑块上有
”形的光滑长直导轨槽,槽口向上,槽内放置一金属滑块,滑块上有 ”形槽的宽度略小.现有半径为r(r<R)
”形槽的宽度略小.现有半径为r(r<R) 如图所示,半圆形半滑凹槽放在光滑的水平面上,小滑块从凹槽边缘A点由静止释放经最低点B,又向上到达另一侧边缘C.把从A点到达B点称为过程I,从B点到达C点称为过程II,则( )
如图所示,半圆形半滑凹槽放在光滑的水平面上,小滑块从凹槽边缘A点由静止释放经最低点B,又向上到达另一侧边缘C.把从A点到达B点称为过程I,从B点到达C点称为过程II,则( ) ”形的光滑长直导轨槽,槽口向上(图为俯视图).槽内放置一个木质滑块,滑块的左半部是半径为R的半圆柱形光滑凹槽,木质滑块的宽度为2R,比“
”形的光滑长直导轨槽,槽口向上(图为俯视图).槽内放置一个木质滑块,滑块的左半部是半径为R的半圆柱形光滑凹槽,木质滑块的宽度为2R,比“ ”形槽的内侧宽度略小.现有一半径为r(r<<R)的金属小球以水平初速度v0冲向滑块,从滑块的一侧半圆形槽口边缘进入.已知金属小球的质量为m,木质滑块的质量为5m,整个运动过程中无机械能损失.求:
”形槽的内侧宽度略小.现有一半径为r(r<<R)的金属小球以水平初速度v0冲向滑块,从滑块的一侧半圆形槽口边缘进入.已知金属小球的质量为m,木质滑块的质量为5m,整个运动过程中无机械能损失.求: