题目内容
如图所示，光滑小球从a处无初速度释放，它可以直接下落，也可以沿光滑斜面ac、ad、ae滑到传送带上，已知ac、ad、ae与竖直方向的夹角分别是15°、30°、45°，传送带与水平方向的夹角θ=30°，则小球以最短的时间到达传送带的路径是（ ）
| A．ab | B．ac | C．ad | D．ae |
设ac的长度为x，知ab、ad的长度相同，xab=xad=
，xae=
．根据牛顿第二定律得，ab=g，ac=gsin75°，ad=gsin60°，ae=gsin45°．
根据x=
at2得，ta=
=
，tc=
，td=
，te=
，比较知tc最小．故B正确，A、C、D错误．
故选B．
| x |
| cos15° |
| x |
| cos30° |
根据x=
| 1 |
| 2 |
|
|
|
|
|
故选B．
练习册系列答案
相关题目
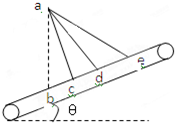如图所示，光滑小球从a处无初速度释放，它可以直接下落，也可以沿光滑斜面ac、ad、ae滑到传送带上，已知ac、ad、ae与竖直方向的夹角分别是15°、30°、45°，传送带与水平方向的夹角θ=30°，则小球以最短的时间到达传送带的路径是（ ）
