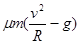题目内容
质量为m的滑块从固定在水平面上、半径为R的半球形碗的边缘由静止滑向碗底，过碗底的速度为，若滑块与碗之间的动摩擦因数为μ，则在过碗底时滑块受到摩擦力的大小为（ ）
分析：滑块经过碗底时，由重力和碗底对球支持力的合力提供向心力，根据牛顿第二定律求出碗底对球的支持力，再由摩擦力公式求解在过碗底时滑块受到摩擦力的大小．
解答：解：滑块经过碗底时，由重力和支持力的合力提供向心力，根据牛顿第二定律得
FN-mg=m
则碗底对球支持力FN=mg+m
所以在过碗底时滑块受到摩擦力的大小f=μFN=μ（mg+m
）=μm（g+
），故C正确，ABD错误；
故选：C．
FN-mg=m
| v2 |
| R |
则碗底对球支持力FN=mg+m
| v2 |
| R |
所以在过碗底时滑块受到摩擦力的大小f=μFN=μ（mg+m
| v2 |
| R |
| v2 |
| R |
故选：C．
点评：本题运用牛顿第二定律研究圆周运动物体受力情况，注意向心力的方向及谁提供向心力是解题的关键，并注意滑动摩擦力的公式．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
如图所示，质量为m的滑块从斜面底端以平行于斜面的初速度v0冲上固定斜面，沿斜面上升的最大高度为H．已知斜面倾角为α，斜面与滑块间的摩擦因数为μ，且μ＜tanα，最大静摩擦力等于滑动摩擦力，取斜面底端为零势能面，则能表示滑块在斜面上运动的机械能E、动能Ek、势能Ep与上升高度h之间关系的图象是（ ）
如图，在水平地面上固定一倾角为θ的斜面，一轻质弹簧的一端固定在斜面底端，整根弹簧处于自然状态．滑块与斜面间动摩擦因素为μ且μ＜tanθ，一质量为m的滑块从距离弹簧上端为S0处的A点由静止释放，设滑块与弹簧接触过程中没有机械能损失，弹簧始终处在弹性限度内，重力加速度大小为g．
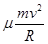C. 
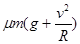D.
