题目内容
8. 如图所示,两个完全相间的长木板A,B靠在一起放在光滑的水平面上,A、B的长均为L=1m,质量均为m=1kg,质量也为m=1kg,物块C放在长木板A点的左端,现给C施加一个水平向右、大小等于10N的恒定拉力F,当C运动到A板的右端时,撤去拉力,结果物块最后滑到B木板的右端时与B木板相对静止,物块C与木板A间的动摩擦因数为μ=0.5,重力加速度为g=10m/s2,不计滑块C的大小.求:
如图所示,两个完全相间的长木板A,B靠在一起放在光滑的水平面上,A、B的长均为L=1m,质量均为m=1kg,质量也为m=1kg,物块C放在长木板A点的左端,现给C施加一个水平向右、大小等于10N的恒定拉力F,当C运动到A板的右端时,撤去拉力,结果物块最后滑到B木板的右端时与B木板相对静止,物块C与木板A间的动摩擦因数为μ=0.5,重力加速度为g=10m/s2,不计滑块C的大小.求:(1)拉力F做的功;
(2)物块C与长木板B的动摩擦因数为多少?
分析 (1)根据牛顿第二定律求得C和AB的我加速度,利用运动学公式求得在拉力F作用下通过的位移,有W=Fx求得拉力做功;
(2)根据牛顿第二定律求得C滑到B上后各自的加速度,利用运动学公式求得摩擦因数
解答 解:(1)当木块C在木板A上运动时,对C根据牛顿第二定律可知F-μmg=ma1,解得${a}_{1}=5m/{s}^{2}$
对AB组成的整体,则μmg=2ma2,解得${a}_{2}=2.5m/{s}^{2}$
时经过时间t1物块C到达木板A的右端,则C运动的位移为${x}_{1}=\frac{1}{2}{{a}_{1}t}_{1}^{2}$
AB运动的位移为${x}_{2}=\frac{1}{2}{{a}_{2}t}_{1}^{2}$
由于L=x1-x2
联立解得${t}_{1}=\frac{2\sqrt{5}}{5}s$
x1=2m
x2=1m
故拉力做功为W=Fx2=10×2J=20J
(2)物块C到达木板A的右端时的速度v=${a}_{1}{t}_{1}=2\sqrt{5}m/s$
木板B的速度$v′=\sqrt{5}m/s$
设木块与B的摩擦因数为μ′,则对木块C可知:-μmg=ma′,解得a′=-μg
对木板Bμmg=ma″,解得a″=μg
根据运动学公式可知v共=v+a′t=v+a″t
解得$t=\frac{\sqrt{5}}{2μg}$,${v}_{共}=\frac{3\sqrt{5}}{2}m/s$
$\frac{{v}_{共}^{2}-{v}^{2}}{2a′}-\frac{{v}_{共}^{2}-v{′}^{2}}{2a″}=L$
联立解得
μ=0.125
答:(1)拉力F做的功为20J;
(2)物块C与长木板B的动摩擦因数为0.125.
点评 本题主要考查了牛顿第二定律和运动学公式,关键是抓住在各阶段物体的加速度,利用好整体法和隔离法即可求得

 如图所示电路中,电源电压u=311sin100πtV,A、B间接有“220V 440W”的电暖宝、“220V 220W”的抽油烟机、交流电压表及保险丝.下列说法正确的是( )
如图所示电路中,电源电压u=311sin100πtV,A、B间接有“220V 440W”的电暖宝、“220V 220W”的抽油烟机、交流电压表及保险丝.下列说法正确的是( )| A. | 交流电压表的示数为220V | |
| B. | 电路要正常工作,保险丝的熔断电流不能小于3$\sqrt{2}$A | |
| C. | 电暖宝发热功率是抽油烟机发热功率的2倍 | |
| D. | 1 min内抽油烟机消耗的电能为1.32×104J |
| A. | 强相互作用力是原子核内部的力,弱相互作用力是原子核外部的力 | |
| B. | 强相互作用力和弱相互作用力都是短程力,其力程均在10-18米范围内 | |
| C. | 每个核子只跟邻近的核子发生核力作用,这种性质称为核力的饱和性 | |
| D. | 组成原子核的核子越多,它的结合能越低 |

(1)通过公式推导验证:在时间内△t,F对导线MN所做的功W等于电路获得的电能W′,也等于导线MN中产生的焦耳热Q.
(2)若导线的质量m=8.0g,长度L=0.1m,感应电流I=1.0A,假设一个原子贡献1个自由电子,计算导线MN中电子沿导线长度方向定向移动的平均速率v(下表中列出了一些你可能用到的数据).
| 阿伏伽德罗常数NA | 6.0×1023mol-1 |
| 元电荷e | 1.6×10-19C |
| 导线MN的摩尔质量μ | 6.0×10-2kg/mol |
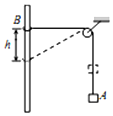 如图所示,物块A和圆环B用绕过定滑轮的轻绳连接在一起,圆环B套在光滑的竖直固定杆上,开始时连接B的绳子处于水平.零时刻由静止释放B,经时间t,B下降h,此时,速度达到最大.不计滑轮摩擦和空气的阻力,则( )
如图所示,物块A和圆环B用绕过定滑轮的轻绳连接在一起,圆环B套在光滑的竖直固定杆上,开始时连接B的绳子处于水平.零时刻由静止释放B,经时间t,B下降h,此时,速度达到最大.不计滑轮摩擦和空气的阻力,则( )| A. | t时刻B的速度大于A的速度 | |
| B. | t时刻B的加速度最大 | |
| C. | 0~t过程A的机械能增加量小于B的机械能减小量 | |
| D. | 0~t过程绳拉力对物块B做的功在数值上等于物块B机械能的减少量 |
 如图所示,两根相同的平行金属导轨固定在水平桌面上,导轨单位长度的电阻相同,端点P、Q用电阻可以忽略的导线相连.垂直于桌面的磁场随时间变化,已知磁感应强度B与时间t的关系为B=kt,比例系数k恒定(k>0).一电阻不计的导体棒可在导轨上无摩擦滑动,在滑动过程中保持与导轨垂直.t=0时刻,导体棒紧靠在P、Q端,在平行于导轨的水平外力F作用下,导体棒以恒定的加速度从静止开始向导轨的另一端滑动,下列关于整个回路的电动势E、电流i、导体棒所受外力F、整个回路消耗的电功率P随时间变化的图象正确的是( )
如图所示,两根相同的平行金属导轨固定在水平桌面上,导轨单位长度的电阻相同,端点P、Q用电阻可以忽略的导线相连.垂直于桌面的磁场随时间变化,已知磁感应强度B与时间t的关系为B=kt,比例系数k恒定(k>0).一电阻不计的导体棒可在导轨上无摩擦滑动,在滑动过程中保持与导轨垂直.t=0时刻,导体棒紧靠在P、Q端,在平行于导轨的水平外力F作用下,导体棒以恒定的加速度从静止开始向导轨的另一端滑动,下列关于整个回路的电动势E、电流i、导体棒所受外力F、整个回路消耗的电功率P随时间变化的图象正确的是( )



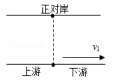 一条河两岸平行,河宽d=80m,河水流速v1=1m/s,一小船在静水中的速度为v2=2m/s.求:
一条河两岸平行,河宽d=80m,河水流速v1=1m/s,一小船在静水中的速度为v2=2m/s.求: