题目内容
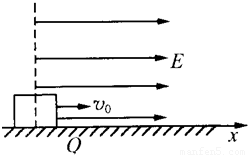
在一个水平面上建立x轴,在过原点O垂直于x轴的平面的右侧空间有一个匀强电场,场强大小E=6×105 N/C,方向与x轴正方向相同,在O处放一个质量m=10g带负电荷的绝缘小物块,其带电量q=5×10-8 C.小物块与水平面间的动摩擦因数μ=0.2,沿x轴正方向给物块一个初速度v=2m/s,如图所示.试求:(1)小物块沿x轴正方向运动离O点的最远距离;
(2)小物块最终停止时的位置.
【答案】分析:(1)物块以初速度v=2m/s沿x轴正方向,受到向左的电场力而匀减速运动,当速度减至零时,小物块沿x轴正方向运动离O点的距离最远,根据动能定理求出此最远的距离.
(2)根据电场力与最大静摩擦力的关系,分析物体能否停在离O点最远的位置.若不能,物块向x轴负方向运动,停在距O点左侧,根据动能定理求出离O点的距离.
解答: 解:(1)当物块沿x轴正方向运动时,受到沿x轴负方向的电场力F和动摩擦力f.电场力大小为F=Eq,滑动摩擦力大小为f=μFN=μmg.
解:(1)当物块沿x轴正方向运动时,受到沿x轴负方向的电场力F和动摩擦力f.电场力大小为F=Eq,滑动摩擦力大小为f=μFN=μmg.
设物块沿x轴正方向运动离O点的最远距离为s,此过程中由动能定理得
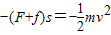
联立解得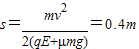
(2)由于F>f,当物块运动到沿x轴正方向运动离O点的最远距离时,又返回向x轴负方向运动,设最终停止时在侧s'处.
在物块向x轴负方向运动的过程中,由动能定理得:
(F-f)s-fs'=0
解得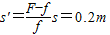
答:(1)小物块沿x轴正方向运动离O点的最远距离为0.4m;
(2)小物块最终停止时的位置在O点左侧0.2m处.
点评:本题涉及力在空间的累积效果,优先考虑动能定理.对于动能定理的应用,关键要选择研究的过程,分析受力情况,确定外力做的总功.
(2)根据电场力与最大静摩擦力的关系,分析物体能否停在离O点最远的位置.若不能,物块向x轴负方向运动,停在距O点左侧,根据动能定理求出离O点的距离.
解答:
 解:(1)当物块沿x轴正方向运动时,受到沿x轴负方向的电场力F和动摩擦力f.电场力大小为F=Eq,滑动摩擦力大小为f=μFN=μmg.
解:(1)当物块沿x轴正方向运动时,受到沿x轴负方向的电场力F和动摩擦力f.电场力大小为F=Eq,滑动摩擦力大小为f=μFN=μmg.设物块沿x轴正方向运动离O点的最远距离为s,此过程中由动能定理得
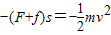
联立解得
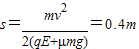
(2)由于F>f,当物块运动到沿x轴正方向运动离O点的最远距离时,又返回向x轴负方向运动,设最终停止时在侧s'处.
在物块向x轴负方向运动的过程中,由动能定理得:
(F-f)s-fs'=0
解得
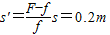
答:(1)小物块沿x轴正方向运动离O点的最远距离为0.4m;
(2)小物块最终停止时的位置在O点左侧0.2m处.
点评:本题涉及力在空间的累积效果,优先考虑动能定理.对于动能定理的应用,关键要选择研究的过程,分析受力情况,确定外力做的总功.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2006?松江区二模)在一个水平面上建立x轴,在过原点O垂直于x轴的平面的右侧空间有一个匀强电场,场强大小E=6×105 N/C,方向与x轴正方向相同,在O处放一个质量m=10g带负电荷的绝缘小物块,其带电量q=5×10-8 C.小物块与水平面间的动摩擦因数μ=0.2,沿x轴正方向给物块一个初速度v0=2m/s,如图所示.试求:
(2006?松江区二模)在一个水平面上建立x轴,在过原点O垂直于x轴的平面的右侧空间有一个匀强电场,场强大小E=6×105 N/C,方向与x轴正方向相同,在O处放一个质量m=10g带负电荷的绝缘小物块,其带电量q=5×10-8 C.小物块与水平面间的动摩擦因数μ=0.2,沿x轴正方向给物块一个初速度v0=2m/s,如图所示.试求: (2007?深圳模拟)在一个水平面上建立x轴,在过原点O垂直于x轴的平面的右侧空间有一匀强电场,场强大小E=6×105N/C,方向与x轴正方向相同,在O处放一个带负电q=5×10-8C,质量为m=10g的绝缘物块(可看作质点),物块与水平面间的动摩擦因数μ=0.2,沿x轴正方向给物块一个初速度v0=2m/s,如图所示,求物块最终停止时的位置.
(2007?深圳模拟)在一个水平面上建立x轴,在过原点O垂直于x轴的平面的右侧空间有一匀强电场,场强大小E=6×105N/C,方向与x轴正方向相同,在O处放一个带负电q=5×10-8C,质量为m=10g的绝缘物块(可看作质点),物块与水平面间的动摩擦因数μ=0.2,沿x轴正方向给物块一个初速度v0=2m/s,如图所示,求物块最终停止时的位置. (2011?永春县模拟)在一个水平面上建立x轴,过原点O垂直于x轴平面的右侧空间有一匀强电场,场强大小E=6×105 N/C,方向与x轴正方向相同.在O处放一个电荷量q=-5×10-6C,质量m=10g的绝缘物块,物块与水平面间的动摩擦因数μ=0.2,沿x轴正方向给物块一个初速度v0=2m/s,如图所示.求物块最终停止时的位置及整个过程运动的路程.(g取10m/s2)
(2011?永春县模拟)在一个水平面上建立x轴,过原点O垂直于x轴平面的右侧空间有一匀强电场,场强大小E=6×105 N/C,方向与x轴正方向相同.在O处放一个电荷量q=-5×10-6C,质量m=10g的绝缘物块,物块与水平面间的动摩擦因数μ=0.2,沿x轴正方向给物块一个初速度v0=2m/s,如图所示.求物块最终停止时的位置及整个过程运动的路程.(g取10m/s2) 在一个水平面上建立x轴,在过原点O垂直于x轴的平面的右侧空间有一个匀强电场,场强大小E=6×105N/C,方向与x轴正方向相同,在原点O处放一个质量m=0.01kg带负电荷的绝缘物块,其带电量q=-5×10-8C.物块与水平面间的动摩擦因数μ=0.2,给物块一个沿x轴正方向的初速度v0=2m/s.如图所示.试求:
在一个水平面上建立x轴,在过原点O垂直于x轴的平面的右侧空间有一个匀强电场,场强大小E=6×105N/C,方向与x轴正方向相同,在原点O处放一个质量m=0.01kg带负电荷的绝缘物块,其带电量q=-5×10-8C.物块与水平面间的动摩擦因数μ=0.2,给物块一个沿x轴正方向的初速度v0=2m/s.如图所示.试求: 如图所示,在一个水平面上建立x轴,在过原点O垂直于x轴的平面的右侧空间有一个匀强电场,场强大小E=6.0×105N/C,方向与x轴正方向相同.在O处放一个电荷量-5.0×10-8C、质量m=1.0×10-2kg的绝缘物块.物块与水平面间的动摩擦因数μ=0.20,沿x轴正方向给物块一个初速度v0=4.0m/s,求物块最终停止时的位置.(g取10m/s2)
如图所示,在一个水平面上建立x轴,在过原点O垂直于x轴的平面的右侧空间有一个匀强电场,场强大小E=6.0×105N/C,方向与x轴正方向相同.在O处放一个电荷量-5.0×10-8C、质量m=1.0×10-2kg的绝缘物块.物块与水平面间的动摩擦因数μ=0.20,沿x轴正方向给物块一个初速度v0=4.0m/s,求物块最终停止时的位置.(g取10m/s2)