题目内容
发射地球同步卫星时,可认为先将卫星发射至距地面高度为h1的圆形轨道上,在卫星经过A点时点火(喷气发动机工作)实施变轨进入椭圆轨道,椭圆轨道的近地点为A,远地点为B.在卫星沿椭圆轨道运动经过B点再次点火实施变轨,将卫星送入同步轨道(远地点B在同步轨道上),如图所示.两次点火过程都是使卫星沿切向方向加速,并且点火时间很短.已知同步卫星的运动周期为T,地球的半径为R,地球表面重力加速度为g,求:
(1)地球的第一宇宙速度
(2)卫星在圆形轨道运行接近A点时的加速度大小;
(3)卫星同步轨道距地面的高度.
(1)地球的第一宇宙速度
(2)卫星在圆形轨道运行接近A点时的加速度大小;
(3)卫星同步轨道距地面的高度.

(1)卫星作圆周运动向心力由重力提供即:
mg=m
解得:v=
(2)设地球质量为M,卫星质量为m,万有引力常量为G、卫星在近地圆轨道运动接近A点时的加速度为aA,在A点万有引力提供圆周运动向心力有:
G
=maA ①
又因为物体在地球表面上受到的万有引力等于重力
G
=mg ②
由①和②解得:aA=
g
(3)设同步轨道距地面高度为h2,根据万有引力提供向心力有:、
G
=m(R+h2)
③
由②③两式解得:h2=
-R
答:(1)地球的第一宇宙速度v=
(2)卫星在圆形轨道运行接近A点时的加速度大小为aA=
g;
(3)卫星同步轨道距地面的高度h2=
-R.
mg=m
| v2 |
| R |
解得:v=
| gR |
(2)设地球质量为M,卫星质量为m,万有引力常量为G、卫星在近地圆轨道运动接近A点时的加速度为aA,在A点万有引力提供圆周运动向心力有:
G
| Mm |
| (R+h1)2 |
又因为物体在地球表面上受到的万有引力等于重力
G
| Mm |
| R2 |
由①和②解得:aA=
| R2 |
| (R+h1)2 |
(3)设同步轨道距地面高度为h2,根据万有引力提供向心力有:、
G
| Mm |
| (R+h2)2 |
| 4π2 |
| T2 |
由②③两式解得:h2=
| 3 |
| ||
答:(1)地球的第一宇宙速度v=
| gR |
(2)卫星在圆形轨道运行接近A点时的加速度大小为aA=
| R2 |
| (R+h1)2 |
(3)卫星同步轨道距地面的高度h2=
| 3 |
| ||

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 如图所示,发射地球同步卫星时,先将卫星发射至近地圆轨道1,到达轨道的Q点时经点火将卫星送入椭圆轨道2,到达轨道的P点时再次点火,将卫星送入同步轨道3.轨道1、2相切于Q点,2、3相切于P点.下列说法中正确的是( )
如图所示,发射地球同步卫星时,先将卫星发射至近地圆轨道1,到达轨道的Q点时经点火将卫星送入椭圆轨道2,到达轨道的P点时再次点火,将卫星送入同步轨道3.轨道1、2相切于Q点,2、3相切于P点.下列说法中正确的是( ) 如图所示,发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步轨道3.轨道1、2相切于Q点,轨道2、3相切于P点(如图所示)则当卫星分别在1、2、3轨道正常运行时,以下说法正确的是( )
如图所示,发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步轨道3.轨道1、2相切于Q点,轨道2、3相切于P点(如图所示)则当卫星分别在1、2、3轨道正常运行时,以下说法正确的是( ) 发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送人同步圆轨道3,轨道1、2相切于Q点,轨道2、3相切于P点.如图所示,则卫星分别在1、2、3轨道上运行时,以下说法正确的是( )
发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送人同步圆轨道3,轨道1、2相切于Q点,轨道2、3相切于P点.如图所示,则卫星分别在1、2、3轨道上运行时,以下说法正确的是( )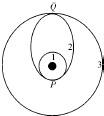 中围自主研制的北斗二号系列卫星预计在2015年形成覆盖全球的卫星导航定位系统.这个系统由三十几颗卫星组成,规划相继发射5颗静止轨道卫星和30颗非静止轨道卫星,建成覆盖全球的北斗卫星导航系统.按照建设规划,201 2年左右,北斗卫星导航系统将首先提供覆盖亚太地区的导航、授时和短报文通信服务能力.2020年左右,建成覆盖全球的北斗卫星导航系统.发射地球同步卫星时,先将其送入近地轨道“l“(轨道半径r1,运行周期T1),然后通过变轨技术进入椭圆轨道“2“(轨道半长轴r2,周期T2),最后才定点进入同步轨道“3“(轨道半径r3,周期T3),P、Q分别为不同轨道的相切点,那么以下说法正确的是( )
中围自主研制的北斗二号系列卫星预计在2015年形成覆盖全球的卫星导航定位系统.这个系统由三十几颗卫星组成,规划相继发射5颗静止轨道卫星和30颗非静止轨道卫星,建成覆盖全球的北斗卫星导航系统.按照建设规划,201 2年左右,北斗卫星导航系统将首先提供覆盖亚太地区的导航、授时和短报文通信服务能力.2020年左右,建成覆盖全球的北斗卫星导航系统.发射地球同步卫星时,先将其送入近地轨道“l“(轨道半径r1,运行周期T1),然后通过变轨技术进入椭圆轨道“2“(轨道半长轴r2,周期T2),最后才定点进入同步轨道“3“(轨道半径r3,周期T3),P、Q分别为不同轨道的相切点,那么以下说法正确的是( ) 发射地球同步卫星时,先将卫星发射到近地圆轨道1,然后点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送人同步圆轨道3.轨道1、2相切于Q点,轨道2、3相切于P点,如图所示,则当卫星分别在1、2、3轨道上正常运行时,下列说法中正确的是( )
发射地球同步卫星时,先将卫星发射到近地圆轨道1,然后点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送人同步圆轨道3.轨道1、2相切于Q点,轨道2、3相切于P点,如图所示,则当卫星分别在1、2、3轨道上正常运行时,下列说法中正确的是( )