题目内容
如图所示，一物体以100J的初动能，从斜面底端的A点沿斜面向上作匀减速直线运动，它经过B点时，动能减少了80J，机械能减少了32J．已知A、B间的距离s＝2m，试求：
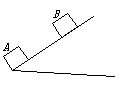
(1)物体沿斜面运动中所受到的滑动摩擦力f的大小是多少？
(2)物体沿斜面向上运动达到最高处时所具有的重力势能是多少？
(3)物体从最高点沿原路下滑到A点时的动能是多少？
答案：
解析：
解析：
解：(1)机械能通过滑动磨擦力做功转化为内能，即有 ΔE机＝fs 解得：f＝ (2)设物体所受的合力为F，对s段和x段用动能定理可得 Fs＝ΔEK1＝80J………………………① Fx＝ΔEK2＝20J………………………② 由上述式①、式②两式得 x＝0.5m 从A点运动到最高点，物体克服摩擦力所做的功为 W＝f(s＋x)＝16×2.5＝40(J) 这40J是变为内能的那部分机械能，其余的部分为重力势能Ep，因此有 EP＝EKA－W＝100－40＝60(J) (3)物体从最高点下滑至A点，克服摩擦力做功仍为40J，即机械能再损失40J，所以物体的末动能为 EK＝EP－W＝60－40＝20(J)
|
＝
＝16(N)
练习册系列答案
相关题目
如图所示，一物体以沿斜面向上的速度从A点沿光滑斜面上滑，最远可达C点，B为AC的中点，已知物体从A到B所用的时间为t，则（ ）
如图所示，一物体以100J的初动能，从斜面底端的A点沿斜面向上作匀减速直线运动，它经过B点时，动能减少了80J，势能增加了48J，已知A、B间的距离s=2m，试求：
如图所示，一物体以初速度V0=10m/s冲上长度为SAB=5m的粗糙斜面，斜面与水平面的夹角=37°，斜面的末端B与传送带用光滑弧形相接，传送带始终保持v=2m/s的速率顺时针运行．已知传送带长度SBC=3m，物体与斜面及传送带间的动摩擦因数均为=0.5．试求：
斜面固定在水平地面上，倾角θ=53°，斜面足够长，物体与斜面间的动摩擦因数μ=0.8，如图所示．一物体以v0=6.4m/s的初速度从斜面底端向上滑行，sin53°=0.8，cos53°=0.6，g取10m/s2，求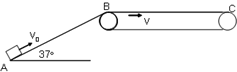
如图所示，一物体以初速度v0=10m/s冲上长度为SAB=3.2m的粗糙斜面，斜面与水平面的夹角θ=37°，斜面的末端B与传送带用光滑弧形相接，假设物体滑到B以后速度大小不变，方向马上变为水平向右，传送带始终保持v=2m/s的速率顺时针运行．已知传送带长度SBC=5m，物体与斜面及传送带间的动摩擦因数均为μ=0.5．试求：（其中g=10m/s2，sin37°=0.6，cos37°=0.8）