题目内容
2010年10月1日在我国西昌卫星发射中心成功发射了“嫦娥二号”探月卫星，其环月飞行的高度距离月球表面100km，所探测到的有关月球的数据比环月飞行高度为200km的嫦娥一号更加翔实．若两颗卫星环月运行均可视为匀速圆周运动，运行轨道如图所示，则（ ）分析：根据月球对嫦娥卫星的万有引力提供向心力，可分别得到周期、线速度、角速度、向心加速度与轨道半径的关系来分析．
解答：解：根据万有引力提供向心力，G
=m
r=ma，得：T=2πr
，a=
．
可知轨道半径r越大，周期越大，向心加速度越小，所以嫦娥二号环月运行的周期比嫦娥一号小，向心加速度比嫦娥一号大．故A正确，B、C、D错误．
故选A．
| Mm |
| r2 |
| 4π2 |
| T2 |
|
| GM |
| r2 |
可知轨道半径r越大，周期越大，向心加速度越小，所以嫦娥二号环月运行的周期比嫦娥一号小，向心加速度比嫦娥一号大．故A正确，B、C、D错误．
故选A．
点评：解决本题的关键利用根据万有引力提供向心力，列式后再进行分析．
练习册系列答案
阅读快车系列答案
相关题目
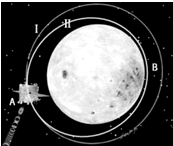2010年10月1日，“嫦娥二号”卫星发射成功．作为我国探月工程二期的技术先导星，“嫦娥二号”的主要任务是为“嫦娥三号”实现月面软着陆开展部分关键技术试验，并继续进行月球科学探测和研究．如图所示，“嫦娥二号”卫星的工作轨道是100km环月圆轨道Ⅰ，为对“嫦娥三号”的预选着陆区--月球虹湾地区（图中B点正下方）进行精细成像，“嫦娥二号”在A点将轨道变为椭圆轨道Ⅱ，使其近月点在虹湾地区正上方B点，大约距月面15km．下列说法中正确的是（ ）
“嫦娥二号”探月卫星于2010年10月1日18时59分在西昌卫星中心发射升空，沿地月转移轨道直奔月球，6日在距月球表面100km的近月点P处，第一次“刹车制动”后被月球捕获，进入椭圆轨道I绕月飞行．这次减速只有一次机会，如果“刹车”力度不够，卫星会飞出月球的引力范围，不被月球捕获，从而不能环绕月球运动．如果刹车力度过大，卫星就可能撞上月球，其后果同样不堪设想．之后卫星在P点又经过两次“刹车制动”，最后在距月球表面100km的圆形轨道Ⅲ上绕月球做匀速圆周运动，其整个过程的运动轨迹如图所示．下列说法中正确的是（ ）
2010年10月1日18时59分57秒，我国在西昌卫星发射中心用“长征三号丙”运载火箭将“嫦娥二号”卫星成功送入太空．已知地球自转周期 T0，月球半径R，卫星距离月球表面的高度h，月球表面的重力加速度g，万有引力常量G．下列说法中正确的是（ ）
A、月球的质量M=
| ||||||
B、卫星的角速度与地球自转的角速度之比为
| ||||||
C、月球的密度ρ=
| ||||||
D、卫星绕月球运行的速率v=
|