题目内容
如图所示的波形图，质点C经过0.5s时间后恰好运动到图中点（4，3）位置，则这列波可能的周期是 s，最小波速是 m/s．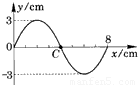
【答案】分析：由题，质点C经过0.5s时间后恰好运动到图中点（4，3）位置，即到达波峰位置，而质点C到达波峰的最短时间为
T或
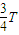，即可得到周期的两个通项；读出波长，求得波速的通项，得到最小波速．
解答：解：若波向右传播，图中C点向上振动，则有 0.5s=（k+
）T，得T=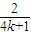
s（k=0、1、2…），波速为v=
=
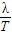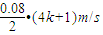=0.04（4k+1）m/s，最小波速为vmin=0.04m/s；
若波向左传播，图中C点向下振动，则有 0.5s=（k+
）T，得T=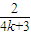
s（k=0、1、2…），波速为v=
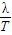=0.04（4k+3）m/s，最小波速为vmin=0.12m/s；
故答案为：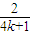
s或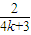
s，（k=0、1、2…），0.04或0.12
点评：本题关键要抓住波的双向性和周期性，得到周期的通项和波速的通项，即可求得波速的最小值．
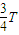T或，即可得到周期的两个通项；读出波长，求得波速的通项，得到最小波速．解答：解：若波向右传播，图中C点向上振动，则有 0.5s=（k+
）T，得T=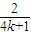s（k=0、1、2…），波速为v=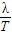==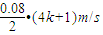0.04（4k+1）m/s，最小波速为vmin=0.04m/s；若波向左传播，图中C点向下振动，则有 0.5s=（k+
）T，得T=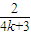s（k=0、1、2…），波速为v=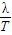=0.04（4k+3）m/s，最小波速为vmin=0.12m/s；故答案为：
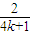s或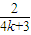s，（k=0、1、2…），0.04或0.12点评：本题关键要抓住波的双向性和周期性，得到周期的通项和波速的通项，即可求得波速的最小值．
练习册系列答案
53天天练系列答案
相关题目
某一简谐横波在t=0s时刻第一次出现如图所示的波形图，再经过△t=1.2s时间，恰好第四次重复出现图示的波形．根据以上信息能确定的是（ ）
⑵将1ml的纯油酸加到500ml的酒精中，待均匀溶解后，用滴管取1ml油酸酒精溶液，让其自然滴出，共200滴．现在让其中一滴落到盛水的浅盘内，待油膜充分展开后，测得油膜的面积为200cm2，则估算油酸分子的大小是 ▲ m（保留一位有效数字）．
的三棱镜．欲使光线从棱镜的侧面AB进入，再直接从侧面AC射出，求入射角θ的取值范围为 ▲ 。
⑴．氦原子被电离一个核外电子，形成类氢结构的氦离子。已知基态的氦离子能量为E1 =－54.4eV，氦离子能级的示意图如图所示。在具有下列能量的光子中，不能被基态氦离子吸收的是 ▲ 
，放出一个速度为2.22×107m/s的粒子，同时产生一个新核
，并释放出频率为ν=3×1019Hz的γ光子。写出这种核反应方程式 ▲ ；这个核反应中产生的新核的速度为 ▲ ；因γ辐射而引起的质量亏损为 ▲ 。(已知普朗克常量h=6.63×10-34J·s)
⑶如图，滑块A、B的质量分别为m1与m2，m1＜m2，置于光滑水平面上，由轻质弹簧相连接，用一轻绳把两滑块拉至最近，弹簧处于最大压缩状态后绑紧，接着使两滑块一起以恒定的速度v0向右滑动．运动中某时刻轻绳突然断开，当弹簧恢复到其自然长度时，滑块A的速度正好为零。则：
⑵将1ml的纯油酸加到500ml的酒精中，待均匀溶解后，用滴管取1ml油酸酒精溶液，让其自然滴出，共200滴．现在让其中一滴落到盛水的浅盘内，待油膜充分展开后，测得油膜的面积为200cm2，则估算油酸分子的大小是 ▲ m（保留一位有效数字）．
的三棱镜．欲使光线从棱镜的侧面AB进入，再直接从侧面AC射出，求入射角θ的取值范围为 ▲ 。
⑴．氦原子被电离一个核外电子，形成类氢结构的氦离子。已知基态的氦离子能量为E1 =－54.4
eV，氦离子能级的示意图如图所示。在具有下列能量的光子中，不能被基态氦离子吸收的是 ▲
，放出一个速度为2.22×107m/s的粒子，同时产生一个新核
，并释放出频率为ν=3×1019Hz的γ光子。写出这种核反应方程式
▲ ；这个核反应中产生的新核的速度为 ▲ ；因γ辐射而引起的质量亏损为 ▲ 。(已知普朗克常量h=6.63×10-34J·s)
⑶如图，滑块A、B的质量分别为m1与m2，m1＜m2，置于光滑水平面上，由轻质弹簧相连接，用一轻绳把两滑块拉至最近，弹簧处于最大压缩状态后绑紧，接着使两滑块一起以恒定的速度v0向右滑动．运动中某时刻轻绳突然断开，当弹簧恢复到其自然长度时，滑块A的速度正好为零。则：