题目内容
 如图,表面光滑的固定斜面顶端安装一定滑轮,小物块A、B用轻绳连接并跨过滑轮(不计滑轮的质量和摩擦).初始时刻,A、B处于同一高度并恰好处于静止状态.剪断轻绳后A下落、B沿斜面下滑,则从剪断轻绳到物体块着地,两物块( )
如图,表面光滑的固定斜面顶端安装一定滑轮,小物块A、B用轻绳连接并跨过滑轮(不计滑轮的质量和摩擦).初始时刻,A、B处于同一高度并恰好处于静止状态.剪断轻绳后A下落、B沿斜面下滑,则从剪断轻绳到物体块着地,两物块( )分析:剪断轻绳后A自由下落,B沿斜面下滑,AB都只有重力做功,机械能守恒,从而可确定落地速度大小关系,及速率变化量;再由牛顿第二定律与运动学公式可确定合力大小与运动时间的关系.
解答:解:设斜面倾角为θ,刚开始AB处于静止状态,所以mBgsinθ=mAg,所以mB>mA,
A、剪断轻绳后A自由下落,B沿斜面下滑,AB都只有重力做功,根据动能定理得:
mv2=mgh
v=
,落地速度大小相等,但方向不同,故A错误;
B、初始时刻,A、B处于同一高度并恰好处于静止状态.当剪断后,两者的合力大小相等,由于质量的不同,所以加速度不同,则运动时间不同.故B正确,D错误;
C、而速度的变化量为v-0=
,即速率的变化量相同,故C错误;
故选B
A、剪断轻绳后A自由下落,B沿斜面下滑,AB都只有重力做功,根据动能定理得:
| 1 |
| 2 |
v=
| 2gh |
B、初始时刻,A、B处于同一高度并恰好处于静止状态.当剪断后,两者的合力大小相等,由于质量的不同,所以加速度不同,则运动时间不同.故B正确,D错误;
C、而速度的变化量为v-0=
| 2gh |
故选B
点评:考查机械能守恒定律的应用,掌握牛顿第二定律与运动学公式的理解,注意两者的质量不同,加速度也不同,但合力大小却相同的细节.

练习册系列答案
相关题目
 如图,表面光滑的固定于水平地面上的斜面的顶端安装一定滑轮,小物块A、B用轻绳连接并跨过滑轮(不计滑轮的质量和摩擦).A、B处于同一高度(取这一高度为0)且恰好保持静止.剪断轻绳后A下落、B沿斜面下滑,空气阻力不计,两物块到达地面时(尚未与地面发生相互作用),它们的( )
如图,表面光滑的固定于水平地面上的斜面的顶端安装一定滑轮,小物块A、B用轻绳连接并跨过滑轮(不计滑轮的质量和摩擦).A、B处于同一高度(取这一高度为0)且恰好保持静止.剪断轻绳后A下落、B沿斜面下滑,空气阻力不计,两物块到达地面时(尚未与地面发生相互作用),它们的( )| A、速度相等 | B、机械能不同 | C、重力势能相同 | D、重力的功率相同 |
 如图,表面光滑的固定斜面顶端安装一定滑轮,小物块A、B用轻绳连接并跨过滑轮(不计滑轮的质量和摩擦).初始时刻,A、B处于同一高度并恰好静止状态.剪断轻绳后A下落、B沿斜面下滑,则从剪断轻绳到物块着地,两物块( )
如图,表面光滑的固定斜面顶端安装一定滑轮,小物块A、B用轻绳连接并跨过滑轮(不计滑轮的质量和摩擦).初始时刻,A、B处于同一高度并恰好静止状态.剪断轻绳后A下落、B沿斜面下滑,则从剪断轻绳到物块着地,两物块( )| A、速率的变化量不同 | B、机械能的变化量不同 | C、重力势能的变化量不相同 | D、重力做功的平均功率不相同 |
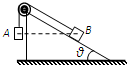 (2012?福建)如图,表面光滑的固定斜面顶端安装一定滑轮,小物块A、B用轻绳连接并跨过滑轮(不计滑轮的质量和摩擦).初始时刻,A、B处于同一高度并恰好处于静止状态.剪断轻绳后A下落、B沿斜面下滑,则从剪断轻绳到物块着地,两物块( )
(2012?福建)如图,表面光滑的固定斜面顶端安装一定滑轮,小物块A、B用轻绳连接并跨过滑轮(不计滑轮的质量和摩擦).初始时刻,A、B处于同一高度并恰好处于静止状态.剪断轻绳后A下落、B沿斜面下滑,则从剪断轻绳到物块着地,两物块( )