题目内容
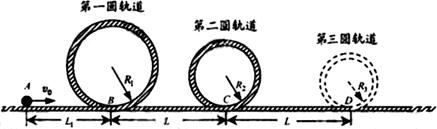
下图是一个设计“过山车”的试验装置的原理示意图。斜面AB与竖直面内的圆形轨道在B点平滑连接。斜面AB和圆形轨道都是光滑的。圆形轨道半径为R。一个质量为m的小车(可视为质点)在A点由静止释放沿斜面滑下，小车恰能通过圆形轨道的最高点Ｃ。已知重力加速度为g。
求：(1)A点距水平面的高度h；
(2)在B点轨道对小车的支持力的大小。
【答案】
（1）h =" 2.5" R（2）FN =" 6" mg
【解析】
试题分析：(1)小车在C点有：mg =
解得：vC =
由A运动到C，根据机械能守恒定律得：mgh = mg×2R+
解得：h =" 2.5" R
(2)由A运动到B，根据机械能守恒定律得：mgh=
解得：vB =
小车在B点有：FN－mg =
解得：FN =" 6" mg
考点：机械能守恒定律的应用
点评：涉及力在空间的效应，要优先考虑机械能守恒．对于圆周运动，涉及力的问题，往往根据向心力进行分析处理．难度适中．
练习册系列答案
相关题目
过山车是游乐场中常见的设施。下图是一种过山车的简易模型，它由水平轨道和在竖直平面内的三个圆形轨道组成，B、C、D分别是三个圆形轨道的最低点，B、C间距与C、D间距相等，半径
、
。一个质量为
kg的小球（视为质点），从轨道的左侧A点以
的初速度沿轨道向右运动，A、B间距
m。小球与水平轨道间的动摩擦因数
，圆形轨道是光滑的。假设水平轨道足够长，圆形轨道间不相互重叠。重力加速度取
，计算结果保留小数点后一位数字。试求
应是多少；
应满足的条件；小球最终停留点与起点
的距离。
应是多少；
的距离。
