题目内容
如图所示是游乐场中过山车的实物图片,可将过山车的一部分运动简化为图12的模型图.模型图中光滑圆形轨道的半径R=8.0m,该光滑圆形轨道固定在倾角为θ=37°斜轨道面上的Q点,圆形轨道的最高点A与倾斜轨道上的P点平齐,圆形轨道与斜轨道之间圆滑连接.现使质量为m的小车(视作质点)从P点以一定的初速度v0=12m/s沿斜面向下运动,不计空气阻力,取g=10m/s2,sin37°=0.6,cos37°=0.8.若小车恰好能通过圆形轨道的最高点A处,则:
(1)小车在A点的速度为多大?(结果用根式表示)
(2)小车在圆形轨道运动时对轨道的最大压力为多少?
(3)求斜轨道面与小车间的动摩擦因数多大?(结果用分数表示)

(1)小车在A点的速度为多大?(结果用根式表示)
(2)小车在圆形轨道运动时对轨道的最大压力为多少?
(3)求斜轨道面与小车间的动摩擦因数多大?(结果用分数表示)

分析:(1)小车恰好能通过圆形轨道的最高点A处,轨道对小车的弹力为零,由重力提供圆周运动所需要的向心力,根据牛顿第二定律求出小车在A点的速度.
(2)根据动能定理或机械能守恒求出小车在轨道B点是的速度,再运用牛顿第二定律,通过支持力和重力的合力提供向心力,求出支持力,由牛顿第三定律得到压力.
(3)对P到A全过程运用动能定理,重力做功为零,根据几何关系求出在斜面上的位移,通过动能定理求出动摩擦因数.
(2)根据动能定理或机械能守恒求出小车在轨道B点是的速度,再运用牛顿第二定律,通过支持力和重力的合力提供向心力,求出支持力,由牛顿第三定律得到压力.
(3)对P到A全过程运用动能定理,重力做功为零,根据几何关系求出在斜面上的位移,通过动能定理求出动摩擦因数.
解答: 解:(1)由于小车恰能通过A点,由重力提供圆周运动所需要的向心力,根据牛顿第二定律得:
解:(1)由于小车恰能通过A点,由重力提供圆周运动所需要的向心力,根据牛顿第二定律得:
mg=m
解得:vA=
=4
m/s…①
(2)如图,小车经轨道最低点D时对轨道压力最大.
设在D点轨道对小车的支持力为N
则有:N-mg=m
…②
小车由D到A的运动过程机械能守恒,
则有:2mgR=
mvD2-
mvA2…③
由①②③得:N=6mg
依牛顿第三定律,在D点小车对轨道的压力N′=N=6mg.
(3)设PQ距离为L,对小车由P到A的过程应用动能定理
得:-μmgLcos37°=
mvA2-
mv02…④
由几何关系得:L=
…⑤
由①、④、⑤解得:μ=
答:
(1)小车在A点的速度为4
m/s.
(2)小车在圆形轨道运动时对轨道的最大压力为6mg.
(3)求斜轨道面与小车间的动摩擦因数为
.
 解:(1)由于小车恰能通过A点,由重力提供圆周运动所需要的向心力,根据牛顿第二定律得:
解:(1)由于小车恰能通过A点,由重力提供圆周运动所需要的向心力,根据牛顿第二定律得:mg=m
| vA2 |
| R |
解得:vA=
| gR |
| 5 |
(2)如图,小车经轨道最低点D时对轨道压力最大.
设在D点轨道对小车的支持力为N
则有:N-mg=m
| vD2 |
| R |
小车由D到A的运动过程机械能守恒,
则有:2mgR=
| 1 |
| 2 |
| 1 |
| 2 |
由①②③得:N=6mg
依牛顿第三定律,在D点小车对轨道的压力N′=N=6mg.
(3)设PQ距离为L,对小车由P到A的过程应用动能定理
得:-μmgLcos37°=
| 1 |
| 2 |
| 1 |
| 2 |
由几何关系得:L=
| R+Rcos37° |
| sin37° |
由①、④、⑤解得:μ=
| 1 |
| 6 |
答:
(1)小车在A点的速度为4
| 5 |
(2)小车在圆形轨道运动时对轨道的最大压力为6mg.
(3)求斜轨道面与小车间的动摩擦因数为
| 1 |
| 6 |
点评:本题综合考查了牛顿第二定律和动能定理,关键是理清运动的过程,运用合适的规律进行求解.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
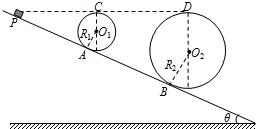 如图所示是游乐场中过山车轨道的模型图.图中半径分别为R1=2.0m和R2=8.0m的两个光滑圆形轨道,固定在倾角为θ=37°斜轨道面上的A、B两点,且与斜轨道之间圆滑连接,两圆形轨道的最高点C、D均与P点平齐.现使小车(视为质点)从P点以一定的
如图所示是游乐场中过山车轨道的模型图.图中半径分别为R1=2.0m和R2=8.0m的两个光滑圆形轨道,固定在倾角为θ=37°斜轨道面上的A、B两点,且与斜轨道之间圆滑连接,两圆形轨道的最高点C、D均与P点平齐.现使小车(视为质点)从P点以一定的 如图所示是游乐场中过山车的模型图,图中半径分别为R1=2.0m和R2=8.0m的两个光滑圆形轨道,固定在倾角为θ=37°斜轨道面上的A、B两点,且两圆形轨道的最高点C、D均与P点平齐,圆形轨道与斜轨道之间圆滑连接,现使小车(视为质点)从P点以一定的初速度沿斜面向下运动,已知斜轨道面与小车间的动摩擦因数为μ=
如图所示是游乐场中过山车的模型图,图中半径分别为R1=2.0m和R2=8.0m的两个光滑圆形轨道,固定在倾角为θ=37°斜轨道面上的A、B两点,且两圆形轨道的最高点C、D均与P点平齐,圆形轨道与斜轨道之间圆滑连接,现使小车(视为质点)从P点以一定的初速度沿斜面向下运动,已知斜轨道面与小车间的动摩擦因数为μ=
