��Ŀ����
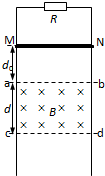 ��ͼ��ʾ��������ֱƽ�з��õĹ⻬�����������ΪL���м����һ��ֵΪR�Ķ�ֵ���裬���������abdc���������ڷֲ��дŸ�Ӧǿ��ΪB����ǿ�ų����ų�����ֱ����ƽ���������Ϊd��һ����Ϊm������Ϊr�ĵ����MN��ֱ���ڵ����ϣ���ų��ϱ߽߱����d0����ʹ��MN�ɾ�ֹ��ʼ�ͷţ���MN�����뿪�ų�ǰ�ѿ�ʼ������ֱ���˶���������費�ƣ������������ʼ�ձ���ˮƽ�����뵼��Ӵ����ã�
��ͼ��ʾ��������ֱƽ�з��õĹ⻬�����������ΪL���м����һ��ֵΪR�Ķ�ֵ���裬���������abdc���������ڷֲ��дŸ�Ӧǿ��ΪB����ǿ�ų����ų�����ֱ����ƽ���������Ϊd��һ����Ϊm������Ϊr�ĵ����MN��ֱ���ڵ����ϣ���ų��ϱ߽߱����d0����ʹ��MN�ɾ�ֹ��ʼ�ͷţ���MN�����뿪�ų�ǰ�ѿ�ʼ������ֱ���˶���������費�ƣ������������ʼ�ձ���ˮƽ�����뵼��Ӵ����ã���1����MN���뿪�ų��±߽�ʱ���ٶȴ�С��
��2����ͨ���ų�����Ĺ����У�����������Ĺ���
��3���Է������۰��ڴų��и��ֿ��ܳ��ֵ��˶���������Ӧ��������
��������1����MN���뿪�ų�ǰ�Ѿ�������ֱ���˶�������ƽ��״̬���ɰ�������ʽ��ƽ����������������뿪�±߽�ʱ���ٶȣ�
��2����MN����ʼ�»������뿪�ų��Ĺ��̣����������غ㶨�ɿ�����������������Ľ����ȣ�
��3�����ݰ�����ų�ʱ���ٶȴ�С�����۰��ڴų��е��˶������
��2����MN����ʼ�»������뿪�ų��Ĺ��̣����������غ㶨�ɿ�����������������Ľ����ȣ�
��3�����ݰ�����ų�ʱ���ٶȴ�С�����۰��ڴų��е��˶������
����⣺��1����MN���뿪�ų��߽�ǰ�������˶����ٶ�Ϊv�������ĵ綯��ΪE=BLv
��·�е��� I=
��MN������ƽ�������� mg-BIL=0
��� v=
��2����MN����ʼ�»������뿪�ų��Ĺ��̣��������غ㶨�ɵã�
mg(d0+d)=E��+
mv2
���������·�в����Ľ�����Ϊ��E��=mg(d0+d)-
���MN��ͨ���ų����Ĺ����в����Ľ����ȣ�E����=
[mg(d0+d)-
]
��3�������������d0�߶���ʱΪt0����d0=
g
��
��t0=
���ڴų�������ʱ�ٶ�Ϊv=
��t=
=
��t0=t����d0=
ʱ��������ų���������ֱ���˶�
��t0��t����d0��
ʱ��������ų������ȼ��ٺ�����ֱ���˶�
��t0��t����d0��
ʱ��������ų������ȼ��ٺ�����ֱ���˶���
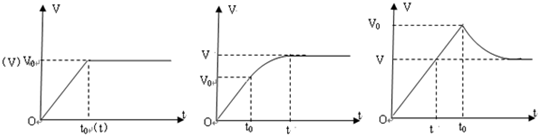
������������߶�d+d0�������ٶ�������߶�h�仯����Ӧ�ĸ��ֿ��ܵ�ͼ����ͼ��ʾ��
��
��1����MN���뿪�ų��±߽�ʱ���ٶ�Ϊv=
��
��2����MN��ͨ���ų����Ĺ����в����Ľ�����ΪE����=
[mg(d0+d)-
]��
��3��d0=
ʱ��������ų���������ֱ���˶�����d0��
ʱ��������ų������ȼ��ٺ�����ֱ���˶�����d0��
ʱ��������ų������ȼ��ٺ�����ֱ���˶���
��·�е��� I=
| E |
| R+r |
��MN������ƽ�������� mg-BIL=0
��� v=
| mg(R+r) |
| B2L2 |
��2����MN����ʼ�»������뿪�ų��Ĺ��̣��������غ㶨�ɵã�
mg(d0+d)=E��+
| 1 |
| 2 |
���������·�в����Ľ�����Ϊ��E��=mg(d0+d)-
| m3g2(R+r)2 |
| 2B4L4 |
���MN��ͨ���ų����Ĺ����в����Ľ����ȣ�E����=
| r |
| R+r |
| m3g2(R+r)2 |
| 2B4L4 |
��3�������������d0�߶���ʱΪt0����d0=
| 1 |
| 2 |
| t | 2 0 |

��t0=
|
���ڴų�������ʱ�ٶ�Ϊv=
| mg(R+r) |
| B2L2 |
��t=
| v |
| g |
| m(R+r) |
| B2L2 |
��t0=t����d0=
| m2g(R+r)2 |
| 2B4L4 |
��t0��t����d0��
| m2g(R+r)2 |
| 2B4L4 |
��t0��t����d0��
| m2g(R+r)2 |
| 2B4L4 |
������������߶�d+d0�������ٶ�������߶�h�仯����Ӧ�ĸ��ֿ��ܵ�ͼ����ͼ��ʾ��
��
��1����MN���뿪�ų��±߽�ʱ���ٶ�Ϊv=
| mg(R+r) |
| B2L2 |
��2����MN��ͨ���ų����Ĺ����в����Ľ�����ΪE����=
| r |
| R+r |
| m3g2(R+r)2 |
| 2B4L4 |
��3��d0=
| m2g(R+r)2 |
| 2B4L4 |
| m2g(R+r)2 |
| 2B4L4 |
| m2g(R+r)2 |
| 2B4L4 |
�������������һ���DZ�����ѵ㣬���ݰ�����ų���ʱ�̽��з�����������ȷ����Ĺؼ���

��ϰ��ϵ�д�
 ���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
�����Ŀ
 ��ͼ��ʾ��������ֱ�̶��Ľ�������ad��bc���l=0.2m����������ˮƽ������MN��EF���ص�����Ħ���ػ�����MN�˺�EF�˵ĵ���ֱ�Ϊ0.2������ֱ��������ĵ��費�ƣ���EF�˷�����ˮƽ��Եƽ̨�ϣ���·NMEF������ǿ�ų��ڣ��ų�����ֱ�ڵ���ƽ������Ÿ�Ӧǿ��B=1T������
��ͼ��ʾ��������ֱ�̶��Ľ�������ad��bc���l=0.2m����������ˮƽ������MN��EF���ص�����Ħ���ػ�����MN�˺�EF�˵ĵ���ֱ�Ϊ0.2������ֱ��������ĵ��費�ƣ���EF�˷�����ˮƽ��Եƽ̨�ϣ���·NMEF������ǿ�ų��ڣ��ų�����ֱ�ڵ���ƽ������Ÿ�Ӧǿ��B=1T������ ��ͼ��ʾ��������ֱ�̶����㹻���Ľ�������ad��bc���L=0.2m����������ˮƽ������MN��EF��������Ϊm=10-2kg�����ص�����Ħ���ػ�����MN�˺�EF�˵ĵ����Ϊ0.2������ֱ��������ĵ��費�ƣ���EF�˷�����ˮƽ��Եƽ̨�ϣ�����װ�ô�����ǿ�ų��ڣ��ų�����ֱ�ڵ���ƽ������Ÿ�Ӧǿ��B=1.0T������MN���ں㶨�����������ɾ�ֹ��ʼ���ϼ����˶�����MN�˼��ٵ�����ٶ�ʱ��EF�˶Ծ�Եƽ̨��ѹ��Ϊ�㣨gȡ10m/s2��
��ͼ��ʾ��������ֱ�̶����㹻���Ľ�������ad��bc���L=0.2m����������ˮƽ������MN��EF��������Ϊm=10-2kg�����ص�����Ħ���ػ�����MN�˺�EF�˵ĵ����Ϊ0.2������ֱ��������ĵ��費�ƣ���EF�˷�����ˮƽ��Եƽ̨�ϣ�����װ�ô�����ǿ�ų��ڣ��ų�����ֱ�ڵ���ƽ������Ÿ�Ӧǿ��B=1.0T������MN���ں㶨�����������ɾ�ֹ��ʼ���ϼ����˶�����MN�˼��ٵ�����ٶ�ʱ��EF�˶Ծ�Եƽ̨��ѹ��Ϊ�㣨gȡ10m/s2��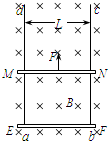 ��ͼ��ʾ��������ֱ�̶����㹻���Ľ�������ad��bc�����ΪL����������ˮƽ������MN��EF���ص�����Ħ���ػ��������ߵ�������Ϊm����������֮�䲿�ֵĵ����ΪR����ֱ��������ĵ��費�ƣ����ռ�����Ŵ�ֱ�ڵ���ƽ��Ĵų����Ÿ�Ӧǿ��ΪB���ų������㹻��ʼʱMN��EF������һ�������ˮƽ��Եƽ̨�ϣ�����һ��ֱ���ϵ�ǣ����ʹMN���ɾ�ֹ��ʼ�ȼ������������ٶȴ�СΪa������
��ͼ��ʾ��������ֱ�̶����㹻���Ľ�������ad��bc�����ΪL����������ˮƽ������MN��EF���ص�����Ħ���ػ��������ߵ�������Ϊm����������֮�䲿�ֵĵ����ΪR����ֱ��������ĵ��費�ƣ����ռ�����Ŵ�ֱ�ڵ���ƽ��Ĵų����Ÿ�Ӧǿ��ΪB���ų������㹻��ʼʱMN��EF������һ�������ˮƽ��Եƽ̨�ϣ�����һ��ֱ���ϵ�ǣ����ʹMN���ɾ�ֹ��ʼ�ȼ������������ٶȴ�СΪa������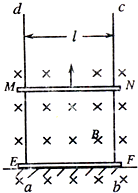 ��ͼ��ʾ��������ֱ�̶����㹻���Ľ�������ad��bc���L=0.2m����������ˮƽ������MN��EF��������Ϊm=10-2kg�����ص�����Ħ���ػ�����MN�˺�EF�˵ĵ����Ϊ0.2������ֱ��������ĵ��費�ƣ���EF�˷�����ˮƽ��Եƽ̨�ϣ�����װ�ô�����ǿ�ų��ڣ��ų�����ֱ�ڵ���ƽ������Ÿ�Ӧǿ��B=1.0T������MN���ں㶨�����������ɾ�ֹ��ʼ���ϼ����˶�����MN�������˶���0.5m���ٶȴﵽ���ʱEF��ǡ�öԾ�Եƽ̨��ѹ��Ϊ�㣮��gȡ10m/s2������
��ͼ��ʾ��������ֱ�̶����㹻���Ľ�������ad��bc���L=0.2m����������ˮƽ������MN��EF��������Ϊm=10-2kg�����ص�����Ħ���ػ�����MN�˺�EF�˵ĵ����Ϊ0.2������ֱ��������ĵ��費�ƣ���EF�˷�����ˮƽ��Եƽ̨�ϣ�����װ�ô�����ǿ�ų��ڣ��ų�����ֱ�ڵ���ƽ������Ÿ�Ӧǿ��B=1.0T������MN���ں㶨�����������ɾ�ֹ��ʼ���ϼ����˶�����MN�������˶���0.5m���ٶȴﵽ���ʱEF��ǡ�öԾ�Եƽ̨��ѹ��Ϊ�㣮��gȡ10m/s2������