题目内容
 如图所示,质量足够大、截面是直角梯形的物块静置在光滑水平地面上,其两个侧面恰合与两个固定在地面上的压力传感器X和Y相接触,图AB高H=0.3m,AD长L=0.5m,斜面倾角θ=37°有一质量m=1kg的小物块p(图中未画出),它与斜面的动磨擦因数μ取sin37°=0.6,cos37°=0.8,重力加速度g=10m/s2.
如图所示,质量足够大、截面是直角梯形的物块静置在光滑水平地面上,其两个侧面恰合与两个固定在地面上的压力传感器X和Y相接触,图AB高H=0.3m,AD长L=0.5m,斜面倾角θ=37°有一质量m=1kg的小物块p(图中未画出),它与斜面的动磨擦因数μ取sin37°=0.6,cos37°=0.8,重力加速度g=10m/s2.(1)在A点给P一个沿斜面向上的初速度v0=3m/s,使之恰好能到达D点,求此时动摩擦因数μ的值;
(2)在第(1)问中若μ=0.5,求p落地时的动能.
分析:(1)根据牛顿第二定律求出加速度的大小,结合位移时间公式求出运动的时间.
(2)根据动能定理求出P上滑到速度为零时经历的位移,对全过程运用动能定理,求出P落地时的动能.
(2)根据动能定理求出P上滑到速度为零时经历的位移,对全过程运用动能定理,求出P落地时的动能.
解答:解:(1)由运动学规律:V02=2aL
得:a=9(m/s2)
又由牛顿第二定律,有a=g(sinθ+μcosθ)
得:μ=
=0.375;
(2)向上运动时,根据牛顿第二定律:a1=
=g(sinθ+μcosθ)=10(m/s2);
则L1=
=0.45(m),
向下运动时,a2=g(sinθ-μcosθ)=2(m/s2)
由速度位移公式:VA2=2a2L1=1.8
根据机械能守恒定律,有
mvA2+mgh=Ek
解得:Ek=3.9(J);
答:(1)在A点给P一个沿斜面向上的初速度v0=3m/s,使之恰好能到达D点,此时动摩擦因数μ的值为0.375;
(2)在第(1)问中若μ=0.5,p落地时的动能为3.9J.
得:a=9(m/s2)
又由牛顿第二定律,有a=g(sinθ+μcosθ)
得:μ=
| 3 |
| 8 |
(2)向上运动时,根据牛顿第二定律:a1=
| mgsinθ+μmgcosθ |
| m |
则L1=
| v02 |
| 2a1 |
向下运动时,a2=g(sinθ-μcosθ)=2(m/s2)
由速度位移公式:VA2=2a2L1=1.8
根据机械能守恒定律,有
| 1 |
| 2 |
解得:Ek=3.9(J);
答:(1)在A点给P一个沿斜面向上的初速度v0=3m/s,使之恰好能到达D点,此时动摩擦因数μ的值为0.375;
(2)在第(1)问中若μ=0.5,p落地时的动能为3.9J.
点评:本题综合考查了牛顿第二定律、动能定理以及运动学公式,综合性较强,对学生的能力要求较高,需加强这方面的训练.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 如图所示,在足够大的光滑水平绝缘桌面上,有两个带电小球A、B,现分别给两球一定的初速度,使其在桌面上运动,如果两者距离始终保持不变,则下列说法不正确的是( )
如图所示,在足够大的光滑水平绝缘桌面上,有两个带电小球A、B,现分别给两球一定的初速度,使其在桌面上运动,如果两者距离始终保持不变,则下列说法不正确的是( )| A、A、B一定带同种电荷 | B、A、B一定带异种电荷 | C、A、B速度始终与两球连线方向垂直 | D、A、B速度大小与其质量成反比 |
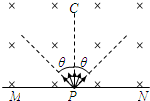 如图所示,在足够大的屏MN的上方有磁感应强度为B的匀强磁场,磁场方向垂直纸面向里,P为屏上一小孔,PC与MN垂直.一束质量为m、电荷量为-q的粒子(不计重力)以相同的速率v从P处射入磁场区域,粒子入射方向在与磁场垂直的平面里,且散开在与PC夹角为θ的范围内,则在屏MN上被粒子打中区域的长度为( )
如图所示,在足够大的屏MN的上方有磁感应强度为B的匀强磁场,磁场方向垂直纸面向里,P为屏上一小孔,PC与MN垂直.一束质量为m、电荷量为-q的粒子(不计重力)以相同的速率v从P处射入磁场区域,粒子入射方向在与磁场垂直的平面里,且散开在与PC夹角为θ的范围内,则在屏MN上被粒子打中区域的长度为( ) (2009?江门一模)如图所示,在足够大的空间范围内,同时存在着竖直向下的匀强电场和垂直纸面向里的水平匀强磁场,磁感应强度B=
(2009?江门一模)如图所示,在足够大的空间范围内,同时存在着竖直向下的匀强电场和垂直纸面向里的水平匀强磁场,磁感应强度B=