题目内容
5.碰撞过程中的能量传递规律在物理学中有着广泛的应用.为了探究这一规律,我们采用多球依次碰撞、碰撞前后速度在同一直线上、且无机械能损失的简化力学模型.如图2所示,在固定光滑水平轨道上,质量分别为m1、m2、m3…mn-1、mn…的若干个球沿直线静止相间排列,给第1个球初能Ek1,从而引起各球的依次碰撞.定义其中第n个球经过依次碰撞后获得的动能Ekn,Ekn与Ek1之比为第1个球对第n个球的动能传递系数k1na、求k1n
b、若m1=4m0,m3=m0,m0为确定的已知量.求m2为何值时,k13值最大.

分析 a、由于两球在碰撞的过程中机械能守恒,同时动量也守恒,列出方程组即可求得碰撞后小球m2的速度大小;
b、根据动能传递系数的定义,求出第n个球的动能,与第1个球的动能相比较即可,再根据得到的结论分析即可求得m2的值.
解答 解:a、设碰撞前m1的速度为v10,根据机械能守恒定律有:
m1gh=$\frac{1}{2}$m1${v}_{10}^{2}$ …①
设碰撞后m1与m2的速度分别为v1和v2,取向右为正方向,根据动量守恒定律有:
m1v10=m1v1+m2v2…②
由于碰撞过程中无机械能损失,有:
$\frac{1}{2}$m1v102=$\frac{1}{2}$m1v12+$\frac{1}{2}$m2v22 …③
②、③式联立解得:v2=$\frac{2{m}_{1}{v}_{10}}{{m}_{1}+{m}_{2}}$…④
将①式代入④式得:v2=$\frac{2{m}_{1}}{{m}_{1}+{m}_{2}}$$\sqrt{2gh}$
(2)①:由④式,考虑到EK1=$\frac{1}{2}$m1${v}_{10}^{2}$和EK2=$\frac{1}{2}{m}_{1}{v}_{2}^{2}$
得:Ek2=$\frac{4{m}_{1}{m}_{2}}{({m}_{1}+{m}_{2})^{2}}{E}_{k1}$
根据动能传递系数的定义,对于1、2两球有:k12=$\frac{{E}_{k2}}{{E}_{k1}}$=$\frac{4{m}_{1}{m}_{2}}{({m}_{1}+{m}_{2})^{2}}$…⑤
同理可得,球m2和球m3碰撞后,动能传递系数k13应为:
k13=$\frac{{E}_{k3}}{{E}_{k1}}$=$\frac{{E}_{k2}}{{E}_{k1}}$•$\frac{{E}_{k3}}{{E}_{k2}}$=$\frac{4{m}_{1}{m}_{2}}{({m}_{1}+{m}_{2})^{2}}$•$\frac{4{m}_{2}{m}_{3}}{({m}_{2}+{m}_{3})^{2}}$…⑥
依此类推,动能传递系数k1n应为:
k1n=$\frac{{E}_{kn}}{{E}_{k1}}$=$\frac{{E}_{k2}}{{E}_{k1}}$•$\frac{{E}_{k3}}{{E}_{k2}}$…$\frac{{E}_{kn}}{{E}_{k(n-1)}}$=$\frac{4{m}_{1}{m}_{2}}{({m}_{1}+{m}_{2})^{2}}$•$\frac{4{m}_{2}{m}_{3}}{({m}_{2}+{m}_{3})^{2}}$•…$\frac{4{m}_{n-1}{m}_{n}}{({m}_{n-1}+{m}_{n})^{2}}$
解得 k1n=$\frac{{4}^{n-1}{m}_{1}{m}_{2}^{2}{m}_{3}^{2}…{m}_{n-1}^{2}{m}_{n}^{\;}}{({m}_{1}+{m}_{2})^{2}({m}_{2}+{m}_{3})^{2}…({m}_{n-1}+{m}_{n})^{2}}$
b、将m1=4m0,m3=m0代入⑥式可得 ${k_{12}}=64m_0^2{[{\frac{m_2}{{(4{m_0}+{m_2})({m_2}+{m_0})}}}]^2}$
为使k13最大,只需使 $\frac{m_2}{{(4{m_0}+{m_2})({m_2}+{m_0})}}=\frac{1}{{{m_2}+\frac{4m_0^2}{m_2}+5{m_0}}}$最大,
即${m_2}+\frac{4m_0^2}{m_2}$取最小值,
由${m_2}+\frac{4m_0^2}{m^2}={({\sqrt{m_2}-\frac{{2{m_0}}}{{\sqrt{m_2}}}})^2}+4{m_0}$可知.
当$\sqrt{m_2}=\frac{{2{m_0}}}{{\sqrt{m_2}}}$,即m2=2m0时,k13最大.
答:a、k1n是$\frac{{4}^{n-1}{m}_{1}{m}_{2}^{2}{m}_{3}^{2}…{m}_{n-1}^{2}{m}_{n}^{\;}}{({m}_{1}+{m}_{2})^{2}({m}_{2}+{m}_{3})^{2}…({m}_{n-1}+{m}_{n})^{2}}$.
b、当m2=2m0 时,k13值最大.
点评 本题目中给的信息比较多,并且是平时不曾遇到的,但是根据题目的信息,逐步分析,根据动能的规律归纳,可求出每个小球的动能,再作比较就能够的出结论.

| A. | 盛有一定质量理想气体的容器在做自由落体运动时,气体对容器仍有压力和压强 | |
| B. | 凡是满足能量守恒的过程都可以自发实现 | |
| C. | 两个分子从相距较远(分子力可忽略)开始靠近,直到不能再靠近的过程中,分子势能先减小后增大 | |
| D. | 用打气筒给自行车轮胎打气,越来越费劲,这是因为分子间斥力增大的缘故 |
| A. | 匀速圆周运动 | B. | 匀减速直线运动 | C. | 匀变速曲线运动 | D. | 类平抛运动 |
 如图所示,一个半径为R的大转盘在水平面内以圆心为轴顺时针匀速转动.一个射击运动员站在转盘边缘上的P点处,随转盘一起做匀速圆周运动,他想用手中的枪射出的子弹击中位于圆心O处的目标.已知大转盘转动的角速度为ω,枪静止不动时射出的子弹初速度为v0,为了击中目标,运动员应该( )
如图所示,一个半径为R的大转盘在水平面内以圆心为轴顺时针匀速转动.一个射击运动员站在转盘边缘上的P点处,随转盘一起做匀速圆周运动,他想用手中的枪射出的子弹击中位于圆心O处的目标.已知大转盘转动的角速度为ω,枪静止不动时射出的子弹初速度为v0,为了击中目标,运动员应该( )| A. | 直接瞄准圆心O处的目标射击 | |
| B. | 瞄准方向应比PO方向向右偏转角度θ=arcsin($\frac{ωR}{{v}_{0}}$) | |
| C. | 瞄准方向应比PO方向向右偏转角度θ=arccos($\frac{ωR}{{v}_{0}}$) | |
| D. | 瞄准方向应比PO方向向右偏转角度θ=arctan($\frac{ωR}{{v}_{0}}$) |
| A. | 光电子的最大初动能之比为2:1 | |
| B. | 该金属的截止频率为$\frac{c}{λ}$ | |
| C. | 用波长为$\frac{5}{2}$λ的单色光照射该金属时能发生光电效应 | |
| D. | 用波长为4λ的单色光照射该金属时不能发生光电效应 |
 如图所示,光滑水平面AB与竖直面内的半圆形导轨在B衔接,导轨半径为R,一个质量为m的静止物体在A处压缩弹簧,在弹力的作用下获得某一向右的速度,当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,之后向上运动恰能完成半圆周运动到达C点,求:
如图所示,光滑水平面AB与竖直面内的半圆形导轨在B衔接,导轨半径为R,一个质量为m的静止物体在A处压缩弹簧,在弹力的作用下获得某一向右的速度,当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,之后向上运动恰能完成半圆周运动到达C点,求: 如图所示,质量M=8kg的长木板放置于光滑的水平面上,其左端有一不计大小,质量为m=2kg的物块,物块与木板间的动摩擦因数为0.2,开始时物块与木板都处于静止状态,现对物块施加F=10N,方向水平向右的恒定拉力,若物块从木板左端运动到右端经历的时间为4秒.设最大静摩擦力等于滑动摩擦力.求:(g取10m/s2)
如图所示,质量M=8kg的长木板放置于光滑的水平面上,其左端有一不计大小,质量为m=2kg的物块,物块与木板间的动摩擦因数为0.2,开始时物块与木板都处于静止状态,现对物块施加F=10N,方向水平向右的恒定拉力,若物块从木板左端运动到右端经历的时间为4秒.设最大静摩擦力等于滑动摩擦力.求:(g取10m/s2)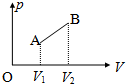 在如图所示的p-V图中,一定质量的理想气体经历AB过程,体积由V1增加到V2,则气体在此过程中发生的变化是( )
在如图所示的p-V图中,一定质量的理想气体经历AB过程,体积由V1增加到V2,则气体在此过程中发生的变化是( )