题目内容
如图，两块相同平板P1，P2置于光滑水平面上，质量均为m．P2的右端固定一轻质弹簧，左端A与弹簧的自由端B相距L．物体P置于P1的最右端，质量为2 m县城可看作质点．P1与P以共同速度v0向右运动，与静止的P2发生碰撞，碰撞时间极短．碰撞后P1与P2粘连在一起．P压缩弹簧后被弹回并停在A点(弹簧始终在弹性限度内)．P与P2之间的动摩擦因数为μ．求
(1)P1、P2刚碰完时的共同速度v1和P的最终速度v2；
(2)此过程中弹簧的最大压缩量x和相应的弹性势能Ep．
答案：
解析：
解析：
|
考点：动量守恒、能量守恒、临界分析 解析：(1)p1和p2碰撞动量守恒： mv0＝(m＋m)v1① 得出： P在p2上滑行过程p1、p2、p系统动量守恒： 2mv0＋2mv1＝4mv2② 得出： (2)p1、p2、p第一次等速弹簧最大压缩量最大，由能量守恒得 p刚进入p2到p1、p2、p第二次等速时有能量守恒得； 由③④得： |
③
④
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
（2013?广东）如图，两块相同平板P1、P2至于光滑水平面上，质量均为m．P2的右端固定一轻质弹簧，左端A与弹簧的自由端B相距L．物体P置于P1的最右端，质量为2m且可以看作质点．P1与P以共同速度v0向右运动，与静止的P2发生碰撞，碰撞时间极短，碰撞后P1与P2粘连在一起，P压缩弹簧后被弹回并停在A点（弹簧始终在弹性限度内）．P与P2之间的动摩擦因数为μ，求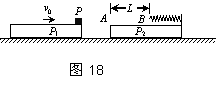
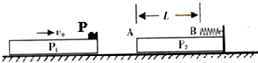如图，两块相同平板P1、P2至于光滑水平面上，质量均为m．P2的右端固定一轻质弹簧，左端A与弹簧的自由端B相距L．物体P置于P1的最右端，质量为2m且可以看作质点．P1与P以共同速度v向右运动，与静止的P2发生碰撞，碰撞时间极短，碰撞后P1与P2粘连在一起，P压缩弹簧后被弹回并停在A点（弹簧始终在弹性限度内）．P与P2之间的动摩擦因数为μ，求