题目内容
20.已知氢原子的基态能量为E1,激发态能量为En=$\frac{{E}_{1}}{{n}^{2}}$(n=2,3,4…),已知普朗克常量为h,真空中光速为c,吸收波长为λ=-$\frac{4hc}{{3E}_{1}}$的光子能使氢原子从基态跃迁到n=2的激发态;此激发态氢原子再吸收一个频率为v的光子后会被电离,则电离后瞬间电子的动能为hv+$\frac{1}{4}$E1.分析 根据能级间跃迁吸收或辐射的光子能量等于两能级间的能级差求出吸收的光子能量,从而得出吸收的波长大小,根据能量守恒求出吸收光子电离后电子的动能.
解答 解:n=2激发态的能量E2=$\frac{1}{4}$E1,
则E2-E1=$\frac{hc}{λ}$=-$\frac{{3E}_{1}}{4}$
解得λ=-$\frac{4hc}{{3E}_{1}}$.
根据能量守恒定律得,hv+E2=$\frac{1}{2}$mv2.
则电子的动能:Ek=hv+$\frac{1}{4}$E1.
故答案为:-$\frac{4hc}{{3E}_{1}}$;hv+$\frac{1}{4}$E1
点评 该题考查氢原子的能级公式和跃迁,解决本题的关键知道能级间跃迁所满足的规律Em-En=hv.

练习册系列答案
相关题目
10.如图甲所示,在匀强磁场中,一矩形金属线框绕与磁场方向垂直的轴匀速转动产生交变电流,电动势e随时间t的变化关系如图乙所示,则( )


| A. | 该交变电流的频率为100Hz | |
| B. | 该交变电流电动势的有效值为311V | |
| C. | t=0.01s时,穿过线框的磁通量为零 | |
| D. | t=0.01s时,穿过线框的磁通量的变化率为零 |
8.关于热现象,下列说法正确的是( )
| A. | 布朗运动就是液体分子的运动 | |
| B. | 自然界中进行的涉及热现象的宏观过程都具有方向性 | |
| C. | 气体吸收热量,内能一定增加 | |
| D. | 气体压强是由气体重力产生的 |
5.已知质量分布均匀的球壳对其内部物体的引力为零,设想在地球赤道正上方高h处和正下方深为h处各修建一绕地心的环形真空轨道,轨道面与赤道面共面,两物件分布在上述两轨道中做匀速圆周运动,轨道对它们均无作用力,设地球半径为R,则( )
| A. | 两物体的速度大小之比为$\frac{R}{{R}^{2}-{h}^{2}}$$\sqrt{(R+h)R}$ | |
| B. | 两物体的速度大小之比为$\frac{R}{{R}^{2}-{h}^{2}}$$\sqrt{Rh}$ | |
| C. | 两物体的加速度大小之比为$\frac{{R}^{3}}{(R+h)^{2}(R-h)}$ | |
| D. | 两物体的加速度大小之比为$\frac{R+h}{R-h}$ |
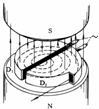
9. 如图所示,用两等长的细绳将一磁铁与一圆形闭合线圈悬于细杆上,静止时线圈平面与磁铁的轴线O1O2垂直,磁铁质量为m,磁极如图所示.在垂直于细杆的平面内,保持细绳绷紧,将磁铁拉至与细杆等高的位置,将磁铁由静止释放,则下列说法正确的是( )
如图所示,用两等长的细绳将一磁铁与一圆形闭合线圈悬于细杆上,静止时线圈平面与磁铁的轴线O1O2垂直,磁铁质量为m,磁极如图所示.在垂直于细杆的平面内,保持细绳绷紧,将磁铁拉至与细杆等高的位置,将磁铁由静止释放,则下列说法正确的是( )
 如图所示,用两等长的细绳将一磁铁与一圆形闭合线圈悬于细杆上,静止时线圈平面与磁铁的轴线O1O2垂直,磁铁质量为m,磁极如图所示.在垂直于细杆的平面内,保持细绳绷紧,将磁铁拉至与细杆等高的位置,将磁铁由静止释放,则下列说法正确的是( )
如图所示,用两等长的细绳将一磁铁与一圆形闭合线圈悬于细杆上,静止时线圈平面与磁铁的轴线O1O2垂直,磁铁质量为m,磁极如图所示.在垂直于细杆的平面内,保持细绳绷紧,将磁铁拉至与细杆等高的位置,将磁铁由静止释放,则下列说法正确的是( )| A. | 磁铁下摆过程中,线圈所受合外力为零 | |
| B. | 磁铁摆到最低点时,两绳子拉力的合力小于3mg | |
| C. | 磁铁下摆过程中,线圈中有逆针方向(沿O1O2方向看)的感应电流 | |
| D. | 磁铁下摆过程中,线圈中有顺时针方向(沿O1O2方向看)的感应电流 |
10.如图,用回旋加速器来加速带电粒子,以下说法正确的是( )

| A. | 图中加速器出口射出的是带正电粒子 | |
| B. | D形盒的狭缝间所加的电压是直流电压 | |
| C. | 强磁场对带电粒子做功,使其动能增大 | |
| D. | 粒子在加速器中的半径越大,周期越长 |
 如图所示,足够长的平行光滑金属导轨竖直放置,轨道间距为l,其上端接一阻值恒为R的灯泡L.在水平虚线L1、L2间有垂直导轨平面的匀强磁场,磁场区域的宽度为d,导体棒a的质量为2m、电阻为R;导体棒b的质量为m、电阻为2R,与导轨始终保持良好接触,它们分别从图中M、N处同时由静止开始沿导轨下滑,且都能匀速穿过磁场区域,当b刚穿过磁场时a正好进入磁场.设重力加速度为g,不计a、b棒之间的相互作用,导体棒始终与导轨垂直.求:
如图所示,足够长的平行光滑金属导轨竖直放置,轨道间距为l,其上端接一阻值恒为R的灯泡L.在水平虚线L1、L2间有垂直导轨平面的匀强磁场,磁场区域的宽度为d,导体棒a的质量为2m、电阻为R;导体棒b的质量为m、电阻为2R,与导轨始终保持良好接触,它们分别从图中M、N处同时由静止开始沿导轨下滑,且都能匀速穿过磁场区域,当b刚穿过磁场时a正好进入磁场.设重力加速度为g,不计a、b棒之间的相互作用,导体棒始终与导轨垂直.求: 如图所示,AOBC为某种透明介质的截面图,△AOC为等腰直角三角形,BC为半径R=10cm的四分之一圆弧,AB与竖直屏MN垂直,屏上A′点为AB延长线与MN的交点,AA′=R,某一单色光射向圆心O,在AB分界面上的入射角i=45°,已知该介质对此光的折射率为n=$\frac{\sqrt{6}}{2}$,求屏MN上光斑与A′的距离.
如图所示,AOBC为某种透明介质的截面图,△AOC为等腰直角三角形,BC为半径R=10cm的四分之一圆弧,AB与竖直屏MN垂直,屏上A′点为AB延长线与MN的交点,AA′=R,某一单色光射向圆心O,在AB分界面上的入射角i=45°,已知该介质对此光的折射率为n=$\frac{\sqrt{6}}{2}$,求屏MN上光斑与A′的距离.