Question

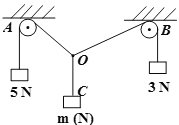
【题目】如图所示，一根绳穿过两个定滑轮，且两端分别挂有和的重物，现在两个滑轮之间的绳上挂一个重量为的物体，恰好使得系统处于平衡状态，求正数的取值范围.

Answer 1

【答案】

【解析】

建立坐标系，设出坐标，把平衡关系转化为向量关系，然后根据三角的相关公式整理出正数关于角的函数，再进行恒等变换求出参数的取值范围.

如图建立坐标系，记OB、OA与轴的正半轴的夹角

分别为，则由三角函数定义得，

，

由于系统处于平衡状态，∴

∴ ，

【方法一】

移项，（1）、（2）平方相加得：，

即 ，

而存在正数使得系统平衡，∴△＝，

∴.（因滑轮大小忽略，写成亦可，

不扣分．这时均为0）

由（*）解得，由（2）式知

∴，这是关于的增函数，

∴正数的取值范围为 .

【方法二】

（1）、（2）平方相加得：，

由（1）知，，而

∴ 随单调递增，∴

（这里的锐角满足，此时）

且（写成不扣分，这时均为0）

∴从而，

∴，即，

∴, ∴正数的取值范围为.