��Ŀ����
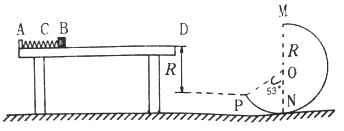
����Ŀ����ͼ��ʾ�����⻬����������費�ƣ����d=2m��������ˮƽ�����=53���ǣ��ڵ����м�δ��ڷ���ֱ��б�����ϡ��Ÿ�Ӧǿ�ȴ�СΪB=1T����ΪL�ij����ε���ǿ�ų�����abcd�������϶����ӵ���R=3����������MN����m=0.25kg�������r=1�����ӵ�������ų��ϱ߽�ab���S=1.0m���ɾ�ֹ�ͷţ����뿪�ų��±߽�ʱ�ٶ�Ϊv=3m/s���ù�����ͨ������R�ĵ���Ϊq=0.3C���������ٶ�g=10m/s2��sin53��=0.8��������MN���˶�����ʼ���뵼�촹ֱ������
(1)�����˸ս���ų�ʱ��R�ϵĵ�����С��
(2)���������е���R�ų���������
(3)�������ų��������õ�ʱ�䡣

���𰸡�(1)2A��(2)1.55625J��(3)0.175s
��������
(1)����ս���ų�ʱ�ٶ�Ϊ![]() ���ɻ�е���غ㶨����
���ɻ�е���غ㶨����
![]()
������
![]()
�����и�Ÿ���
![]()
���ݱպϵ�·ŷķ����
![]()
(2)�����
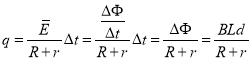
���
![]()
���������غ���
![]()
��Ÿ�Ӧ�����е���R�ϲ�������Ϊ
![]()
(3)ѡȡ��б������Ϊ�����ɶ�������
![]()
��
![]()
������
![]()

��ϰ��ϵ�д�
 Сѧ��10���ӿ������100��ϵ�д�
Сѧ��10���ӿ������100��ϵ�д�
�����Ŀ