题目内容
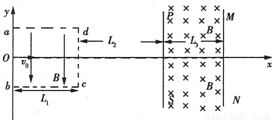
如图所示,正方形区域abcd边长L1=8cm,内有平行于ab方向指向bc边的匀强电场,场强E=3750V/m,一带正电的粒子电荷量q=lO-10C,质量m=10-20㎏,从坐标原点O点开始沿电场中心线(x轴方向)飞入电场,初速度v=2×106m/s.粒子飞出电场后经过界面宽度L2=12cm的cd、PS间的无电场区域后,进入磁感应强度为2.5×lO-3T、宽度为L3=12cm的PS、MN间的匀强磁场区域.试求:(1)粒子穿过界面PS时偏离x轴的距离y;
(2)粒子穿过界面PS时的速度大小与方向;
(3)粒子再一次到达x轴时的位置;
(4)粒子从O点到再次到达x轴上的总时间.
【答案】分析:由题意可知,带电粒子在电场中做类平抛运动,在中间电磁场的区域内做直线运动;在磁场中做匀速圆周运动;则由类平抛及圆周运动的知识,结合几何关系可求得偏转位移及运动时间.
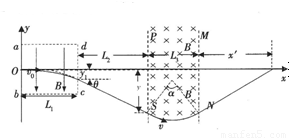
解答:解:粒子运动的轨迹如图所示:
(1)带电粒子在电场中偏转,沿电场方向上电荷做匀加速直线运动,F=Eq;
F=ma;
竖直方向的位移y1= at2=
at2= =0.03m=3cm;
=0.03m=3cm;
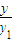 =
=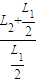 =
=
解得y=4y1=12cm;
(2)而竖直方向vy=at=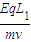 =1.5×106m/s;
=1.5×106m/s;
vx=v=2×106m/s;
粒子的运动速度为v= =2.5×106m/s;
=2.5×106m/s;
粒子的速度偏向角的正切为tanθ=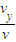 =0.75;
=0.75;
θ=37°;
(3)设粒子在匀强磁场中做圆周运动的半径为R,由Bqv=m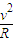 得:
得:
R=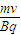 =0.1m=10cm;
=0.1m=10cm;
由几何关系可知,粒子进入磁场的点和射出磁场的点到x轴的距离相等,都为12cm,射出磁场的速度方向与x轴的夹角也为37°,则粒子出磁场后沿水平方向的位移
x′=ycot37°=16cm;
粒子再经过x轴时的位置与O点的距离
x=L1+L2+L3+x′=48cm;
(4)粒子在磁场外运动的时间
t1= =1.8×10-7s;
=1.8×10-7s;
粒子在磁场中运动的圆心角α=2×37°=74°
在磁场中运动的时间t2= ×
× =0.52×10-7s;
=0.52×10-7s;
点评:在本题给定的物理情景中,带电粒子分别经电场和磁场的作用而产生偏转,解题时要注意在两种场中带电粒子运动的性质不同,解题方法不同.
解答:解:粒子运动的轨迹如图所示:

(1)带电粒子在电场中偏转,沿电场方向上电荷做匀加速直线运动,F=Eq;
F=ma;
竖直方向的位移y1=
 at2=
at2= =0.03m=3cm;
=0.03m=3cm;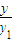 =
=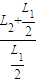 =
=
解得y=4y1=12cm;
(2)而竖直方向vy=at=
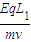 =1.5×106m/s;
=1.5×106m/s;vx=v=2×106m/s;
粒子的运动速度为v=
 =2.5×106m/s;
=2.5×106m/s;粒子的速度偏向角的正切为tanθ=
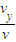 =0.75;
=0.75;θ=37°;
(3)设粒子在匀强磁场中做圆周运动的半径为R,由Bqv=m
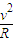 得:
得:R=
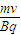 =0.1m=10cm;
=0.1m=10cm;由几何关系可知,粒子进入磁场的点和射出磁场的点到x轴的距离相等,都为12cm,射出磁场的速度方向与x轴的夹角也为37°,则粒子出磁场后沿水平方向的位移
x′=ycot37°=16cm;
粒子再经过x轴时的位置与O点的距离
x=L1+L2+L3+x′=48cm;
(4)粒子在磁场外运动的时间
t1=
 =1.8×10-7s;
=1.8×10-7s;粒子在磁场中运动的圆心角α=2×37°=74°
在磁场中运动的时间t2=
 ×
× =0.52×10-7s;
=0.52×10-7s;点评:在本题给定的物理情景中,带电粒子分别经电场和磁场的作用而产生偏转,解题时要注意在两种场中带电粒子运动的性质不同,解题方法不同.

练习册系列答案
相关题目
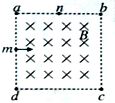 如图所示,正方形区域abcd中充满匀强磁场,磁场方向垂直纸面向里.一个氢核从ad边的中点m沿着既垂直于ad边又垂直于磁场的方向,以一定速度射入磁场,正好从ab边中点n射出磁场.现将磁场的磁感应强度变为原来的2倍,其他条件不变,则下列判断正确的是( )
如图所示,正方形区域abcd中充满匀强磁场,磁场方向垂直纸面向里.一个氢核从ad边的中点m沿着既垂直于ad边又垂直于磁场的方向,以一定速度射入磁场,正好从ab边中点n射出磁场.现将磁场的磁感应强度变为原来的2倍,其他条件不变,则下列判断正确的是( )| A、粒子将从a点射出磁场 | B、粒子将从b射出磁场 | C、粒子在磁场中运动的时间相同 | D、粒子在磁场中运动的时间不同 |

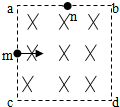 如图所示,正方形区域abcd中充满匀强磁场,磁场方向垂直纸面向里,一个氢核从ac边的中点m沿着既垂直于ac边又垂直磁场的方向,以一定速度射入磁场,正好从ab边中点n射出磁场,若将磁场的磁感应强度变为原来的2倍,其他条件不变,则这个氢核射出磁场的位置是
如图所示,正方形区域abcd中充满匀强磁场,磁场方向垂直纸面向里,一个氢核从ac边的中点m沿着既垂直于ac边又垂直磁场的方向,以一定速度射入磁场,正好从ab边中点n射出磁场,若将磁场的磁感应强度变为原来的2倍,其他条件不变,则这个氢核射出磁场的位置是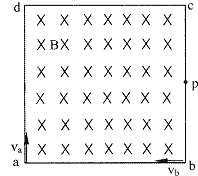 如图所示,正方形区域内有垂直于纸面向里的匀强磁场,磁感应强度为B,两个电子分别从a、b两点沿图示方向射人磁场且恰好在bc边的中点p处相遇,不计两电子间的作用力,不计重力,电子的比荷
如图所示,正方形区域内有垂直于纸面向里的匀强磁场,磁感应强度为B,两个电子分别从a、b两点沿图示方向射人磁场且恰好在bc边的中点p处相遇,不计两电子间的作用力,不计重力,电子的比荷 如图所示,正方形区域MNPQ内有垂直纸面向里的匀强磁场.在外力作用下,一正方形闭合刚性导线框沿QN方向匀速运动,t=0时刻,其四个顶点M′、N′、P′、Q′恰好在磁场边界中点.下列图象中能反映线框所受安培力f的大小随时间t变化规律的是( )
如图所示,正方形区域MNPQ内有垂直纸面向里的匀强磁场.在外力作用下,一正方形闭合刚性导线框沿QN方向匀速运动,t=0时刻,其四个顶点M′、N′、P′、Q′恰好在磁场边界中点.下列图象中能反映线框所受安培力f的大小随时间t变化规律的是( )