Question

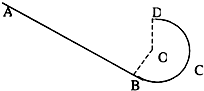如图所示，倾斜轨道 AB 与有缺口的圆轨道 BCD 相切于 B，圆轨道半径为 R，两轨道在同一竖直平面内，D 是圆轨道的最高点（且 OD 竖直），缺口 DB 所对的圆心角为120°，把一个小球从倾斜轨道上由静止释放，它下滑到 B 点后便进入圆轨道，要使它上升到 D 点，不计摩擦，则下列说法中正确的是（　　）

• A．释放点须比 D 点高出 

  R

  2

• B．释放点须比 D 点高出

  R

  4

• C．释放点须与 D 点等高
• D．由于小球质量未知，无法计算释放点的高度

Answer 1

分析：根据牛顿第二定律求出小球上升到 D 点的临界速度．
研究小球从释放点到D点，根据机械能守恒定律求出释放点与 D 点的高度差．

解答：解：小球刚好上升到D点，根据牛顿第二定律得
mg=

mvD2

R

v_D=

gR

①
研究小球从释放点到D点，根据机械能守恒定律得
mgh=

1

2

m

v

2 D

 ②
由①②得h=

R

2

所以释放点须比 D 点高出 

R

2

．
故选A．

点评：该题把圆周运动的临界条件和机械能守恒结合应用．