题目内容
（18分）如图所示，在水平光滑绝缘的桌面上，有三个带正电的质点1、2、3，位于边长为
的等边三角形的三个顶点处。
为三角形的中心，三个质点的质量皆为
，带电量皆为
。质点 1、3之间和2、3之间用绝缘的轻而细的刚性杆相连，在3的连接处为无摩擦的铰链。已知开始时三个质点的速度为零，在此后运动过程中，当质点3运动到C处时，其速度大小为多少？
解析：
以三个质点为系统，由对称性可知，开始时其质心应位于
处，因为质点系所受的合外力为零，由质心运动定理可知，质心总是固定不动的。质点1、2在静电力作用下，彼此间距离必增大，但不可能保持在沿起始状态时1、2连线上运动，若是那样运动，由于杆不能伸长，质点3必向左运动，三者的质心势必亦向左运动，这与“质心不动”相矛盾，故不可能。由此可知，由于杆为刚性，质点1、2在静电力作用下，要保持质心不动，质点1、2必将分别向题图中右上方和右下方运动，而质点3将向左运动．当3运动到处时，1、2将运动到
、
处，、、三点在一直线上，1、2的速度方向向右，3的速度方向左（如图所示）。令
、
、
分别表示此时它们的速度大小，则由对称性可知此时三质点的总动能为
（1）
再由对称性及动量守恒可知
（2）
系统原来的电势能为
（3）
其中
为静电力常数．运动到图所示的位置时的电势能为
（4）
根据能量守恒有
（5）
由以上各式可解得
（6）
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
如图所示，在水平光滑导轨上放置一辆小车，小车上固定一小风扇和一块挡板a其中风扇平面相对小车可以绕竖直轴360°转动，挡板面与导轨垂直，且其面积略大于小风扇吹出的风的面积．当风扇正对着挡板吹风时，小车恰好保持不动．若风扇从正对着挡板吹风开始，然后顺时针缓慢地绕竖直轴转动180°，在此过程中小车（ ）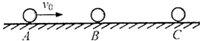
如图所示，在水平光滑直导轨上，静止着三个质量均为m=1kg的相同小球A、B、C，现让A球以v0=2m/s的速度向着B球运动，A、B两球碰撞后粘合在一起，两球继续向右运动并跟C球碰撞，C球的最终速度vC=1m/s．求A、B两球跟C球相碰前的速度和相碰后的速度．
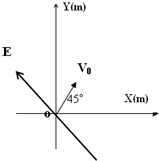如图所示，在水平光滑绝缘平面上，水平匀强电场方向与X轴间成45°角，电场强度E=1×103N/c．某带电小球电量为q=-2×10-6c，质量m=1×10-3kg，以初速度V0=2m/s从坐标轴原点出发，V0与水平匀强电场垂直，当带电小球再经过X轴时与X轴交于A点，求带电小球经过A点时
（选修模块3-5）
合在一起继续向右运动，再跟C球碰撞，C球的最终速度为vC=1m/s．求：