题目内容
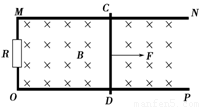
如图所示，电阻不计的平行金属导轨MN和OP放置在水平面内．MO间接有阻值为R＝3 Ω的电阻．导轨相距d＝1 m，其间有竖直向下的匀强磁场，磁感应强度B＝0.5 T．质量为m＝0.1 kg，电阻为r＝1 Ω的导体棒CD垂直于导轨放置，并接触良好．用平行于MN的恒力F＝1 N向右拉动CD.CD受摩擦阻力f恒为0.5 N．求：
1.CD运动的最大速度是多少？
2.当CD到最大速度后，电阻R消耗的电功率是多少？
3.当CD的速度为最大速度的一半时，CD的加速度是多少？
【答案】
1.8 m/s.
2.3 W
3.2.5 m/s2
【解析】(1)设CD棒运动速度为v，
则：导体棒产生的感应电动势为：E＝Bdv①
据闭合电路欧姆定律有：I＝②
则安培力为：F0＝BdI③
据题意分析，当v最大时，有：F－F0－Ff＝0④
联立①②③④得：vm＝＝8 m/s.⑤
(2)棒CD速度最大时同理有：Em＝Bdvm⑥
Im＝⑦
而PRm＝I·R⑧
联立⑤⑥⑦得：PRm＝＝3 W．⑨
(3)当CD速度为vm时有：E′＝Bdvm/2⑩
I＝⑪
F′＝BId⑫
据牛顿第二定律有：F－F′－Ff＝ma⑬
联立⑩⑪⑫⑬⑭得：a＝2.5 m/s2.⑭
练习册系列答案
相关题目
如图所示，电阻不计的平行金属导轨MN和OP水平放置．MO间接有阻值为R的电阻．导轨相距为d，有竖直向下的匀强磁场，磁感强度为B．质量为m，长为L的导体棒CD的电阻为r，垂直于导轨放置，并接触良好．用平行于MN的恒力F向右拉动CD棒．CD棒受恒定的摩擦阻力f．已知F＞f，L＞d，求：
如图所示，电阻不计的平行粗糙长金属导轨固定在一绝缘斜面上，两相同的金属棒a、b垂直于导轨放置，且与导轨良好接触，匀强磁场垂直穿过导轨平面．现用一平行于导轨的恒力F作用在a的中点，使其向上运动．在a运动的整个过程中若b始终保持静止，则它所受摩擦力可能（ ）
如图所示，电阻不计的平行金属导轨MN和OP放置在水平面内，MO间接有阻值为R=3Ω的电阻，导轨相距d=1m，其间有竖直向下的匀强磁场，磁感应强度B=0.5T．质量为m=0.1kg，电阻为r=1Ω的导体棒CD垂直于导轨放置，并接触良好．用平行于MN的恒力F=1N向右拉动CD，CD受摩擦阻力f恒为0.5N．求：（1）CD运动的最大速度；（2）当CD达到最大速度后，电阻R消耗的电功率．
（2013?河南模拟）如图所示，电阻不计的平行光滑金属导轨与水平面的夹角为θ，宽度为l，下端与阻值为R的电阻相连．磁感应强度为B的匀强磁场垂直穿过导轨平面，现使质量为m的导体棒ab位置以平行于斜面的初速度沿导轨向上运动，滑行到最远位置a′b′后又下湍．已知导体棒运动过程中的最大加速度为2gsinθ，g为重力加速度，轨道足够长，则（ ）
（2012?湛江一模）如图所示，电阻不计的光滑平行金属导轨MN和OP水平放置，MO间接有阻值为R的电阻，两导轨相距为L，其间有竖直向下的匀强磁场．质量为m、长度为L、电阻为R0的导体棒CD垂直于导轨放置，并接触良好．在CD的中点处用大小为F平行于MN向右的水平恒力啦CD从静止开始运动s的位移，导体棒CD的速度恰好达到最大速度vm．