题目内容
 某水上游乐场举办了一场趣味水上比赛.如图所示,质量m=50kg的参赛者(可视为质点),在河岸上A点紧握一根长L=5.0m的不可伸长的轻绳,轻绳另一端系在距离水面高H=10.0m的O点,此时轻绳与竖直方向的夹角为θ=37°,C点是位于O点正下方水面上的一点,距离C点x=4.8m处的D点固定着一只救生圈,O、A、C、D各点均在同一竖直面内.若参赛者抓紧绳端点,从台阶上A点沿垂直于轻绳斜向下以一定的初速度跃出,当摆到O点正下方的B点时松开手,此后恰能落在救生圈内.(sin37°=0.6,cos37°=0.8,
某水上游乐场举办了一场趣味水上比赛.如图所示,质量m=50kg的参赛者(可视为质点),在河岸上A点紧握一根长L=5.0m的不可伸长的轻绳,轻绳另一端系在距离水面高H=10.0m的O点,此时轻绳与竖直方向的夹角为θ=37°,C点是位于O点正下方水面上的一点,距离C点x=4.8m处的D点固定着一只救生圈,O、A、C、D各点均在同一竖直面内.若参赛者抓紧绳端点,从台阶上A点沿垂直于轻绳斜向下以一定的初速度跃出,当摆到O点正下方的B点时松开手,此后恰能落在救生圈内.(sin37°=0.6,cos37°=0.8,| 12.96 |
(1)求参赛者经过B点时速度的大小v;
(2)参赛者从台阶上A点跃出时的动能Ek为多大?
(3)沿竖直方向适当调节绳端O点的高度(仍在A点上方),参赛者从A点拉直并抓紧轻绳,由静止开始摆下,经O点正下方松开绳,此后也恰能落在救生圈内.试求参赛者松开绳时距水面的高度h.
分析:(1)人从B向D运动做平抛运动,根据平抛运动的位移公式列式求解即可;
(2)人从A到B过程机械能守恒,根据守恒定律列式求解即可;
(3)根据机械能守恒和平抛运动知识结合求解h.
(2)人从A到B过程机械能守恒,根据守恒定律列式求解即可;
(3)根据机械能守恒和平抛运动知识结合求解h.
解答:解:(1)参赛者从B点到D点做平抛运动
H-L=
gt2 ①
x=vt ②
由①②式代入数据解得 v=4.8m/s
(2)参赛者从A点到B点的过程中,由机械能守恒定律得
mghAB=
mv2-Ek ③
其中 hAB=L(1-cosθ) ④
由③④式代入数据解得 Ek=76J
(3)设参赛者经O点正下方时的速度为v′,则
mv′2=mg(H-Lcos37°-h) ⑤
又x=v′
⑥
由⑤⑥代入数据解得 h=4.8m,h′=1.2m(不合题意舍去)
答:
(1)参赛者经过B点时速度的大小v是4.8m/s;
(2)参赛者从台阶上A点跃出时的动能Ek为76J.
(3)参赛者松开绳时距水面的高度h是4.8m.
H-L=
| 1 |
| 2 |
x=vt ②
由①②式代入数据解得 v=4.8m/s
(2)参赛者从A点到B点的过程中,由机械能守恒定律得
mghAB=
| 1 |
| 2 |
其中 hAB=L(1-cosθ) ④
由③④式代入数据解得 Ek=76J
(3)设参赛者经O点正下方时的速度为v′,则
| 1 |
| 2 |
又x=v′
|
由⑤⑥代入数据解得 h=4.8m,h′=1.2m(不合题意舍去)
答:
(1)参赛者经过B点时速度的大小v是4.8m/s;
(2)参赛者从台阶上A点跃出时的动能Ek为76J.
(3)参赛者松开绳时距水面的高度h是4.8m.
点评:本题是两个过程的问题,运用平抛运动的规律、机械能守恒或动能定理结合进行研究,难度不大.

练习册系列答案
相关题目
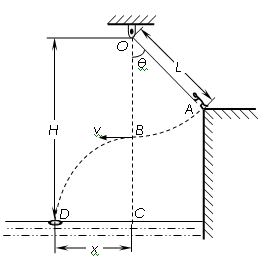
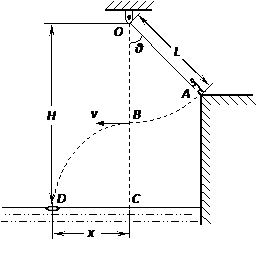
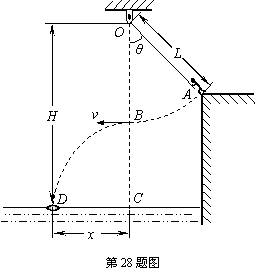 (3)沿竖直方向适当调节绳端O点的高度(仍在A点上方),参赛者从A点拉直并抓紧轻绳,由静止开始摆下,经O点正下方松开绳,此后也恰能落在救生圈内.试求参赛者松开绳时距水面的高度h.
(3)沿竖直方向适当调节绳端O点的高度(仍在A点上方),参赛者从A点拉直并抓紧轻绳,由静止开始摆下,经O点正下方松开绳,此后也恰能落在救生圈内.试求参赛者松开绳时距水面的高度h.