题目内容
如图所示，AB是竖直面内的四分之一圆弧形光滑轨道，下端B与水平直轨道相切．一个小物块自A点由静止开始沿轨道下滑，已知轨道半径为R=0.2m，小物块的质量为m=0.1kg，小物块与水平面间的动摩擦因数µ=0.5，取g=10m/s2．求：（1）小物块到达圆弧轨道末端B点时受支持力．
（2）小物块在水平面上滑动的最大距离．
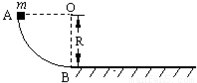
【答案】分析：（1）小物块从A运动到B的过程中只有重力做功，机械能守恒，根据机械能守恒定律求出物块到达圆弧末端B点时的速度，在B点物块受重力和支持力，两个力的合力提供圆周运动的向心力，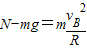
．根据此公式解出支持力N．
（2）从小物块从A点开始运动到停止全过程运用动能定理，在此过程中有重力做功，摩擦力做功，动能的变化为0，根据动能定理求出滑动的最大距离．
解答：解：（1）由机械能守恒定律，得：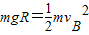
在B点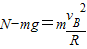
由以上两式得 N=3mg=3N．
故小物块到达圆弧轨道末端B点时受的支持力为3N．
（2）设在水平面上滑动的最大距离为s
由动能定理得 mgR-μmgs=0
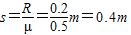
故小物块在水平面上滑动的最大距离为0.4m．
点评：解决本题的关键知道只有重力做功，机械能守恒，掌握运用机械能守恒定律以及动能定理进行解题．
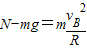．根据此公式解出支持力N．（2）从小物块从A点开始运动到停止全过程运用动能定理，在此过程中有重力做功，摩擦力做功，动能的变化为0，根据动能定理求出滑动的最大距离．
解答：解：（1）由机械能守恒定律，得：
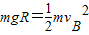
在B点
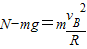
由以上两式得 N=3mg=3N．
故小物块到达圆弧轨道末端B点时受的支持力为3N．
（2）设在水平面上滑动的最大距离为s
由动能定理得 mgR-μmgs=0
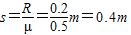
故小物块在水平面上滑动的最大距离为0.4m．
点评：解决本题的关键知道只有重力做功，机械能守恒，掌握运用机械能守恒定律以及动能定理进行解题．
练习册系列答案
相关题目
如图所示，
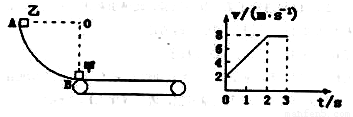
如图所示，AB是竖直平面内的四分之一光滑圆弧，O为圆心，OA水平．一质量m=1kg的小球自圆弧上的A点由静止释放后沿圆弧运动到B点，离开B点后做平抛运动，最终落在地面上的C点，已知B点离地面的高度h=0.8m，BC间的水平距离s=2m，g=10m/s2，求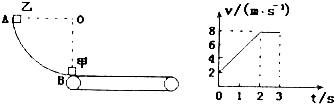
小物块，质量均为0.2kg，在圆轨道的下端B点放置小物块甲，将小物块乙从圆轨道的A端由静止释放，甲和乙碰撞后粘合在一起，它们在传送带上运动的v-t图象如图所示．g=10m/s2，求：
