题目内容
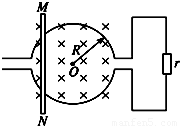
如图所示,半径为R的圆形导轨处在垂直于圆平面的匀强磁场中,磁感应强度为B,方向垂直于纸面向内.一根长度略大于导轨直径的导体棒MN以速率v在圆导轨上从左端滑到右端,电路中的定值电阻为r,其余电阻不计,导体棒与圆形导轨接触良好.求:(1)在滑动过程中通过电阻r的电流的平均值;
(2)MN从左端到右端的整个过程中,通过r的电荷量;
(3)当MN通过圆导轨中心时,通过r的电流是多大?
【答案】分析:(1)导体棒MN切割磁感线产生感应电流,根据法拉第电磁感应定律,从而求出从左端滑到右端导体棒产生的平均感应电动势,再由闭合电路欧姆定律可求出通过电阻的平均电流;
(2)根据法拉第电磁感应定律、欧姆定律、电流与电量的关系式求解通过导体棒的电荷量.
(3)由E=BLv求出导体棒MN通过圆导轨中心时产生的感应电动势,由闭合电路欧姆定律可求出通过电阻的电流.
解答:解:(1)由法拉第电磁感应定律可得: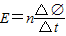 ,
,
则有: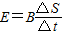
而圆形面积为:△S=πR2
导体棒运动的时间为: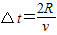
再由闭合电路欧姆定律可得: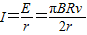
(2)MN从左端到右端的整个过程中,通过r的电荷量:q=It
而闭合电路欧姆定律可得: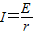
由法拉第电磁感应定律可得: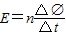
所以q=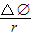 =
=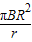
(3)当导体棒MN通过圆导轨中心时,
产生的感应电动势为E=2BRv
由闭合电路欧姆定律可得::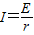
所以通过r的电流:I=2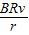
答:(1)在滑动过程中通过电阻r的电流的平均值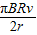 ;
;
(2)MN从左端到右端的整个过程中,通过r的电荷量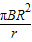 ;
;
(3)当MN通过圆导轨中心时,通过r的电流是2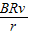 .
.
点评:考查法拉第电磁感应定律、闭合电路欧姆定律,且电量与磁通量的变化及电阻有关.并体现了平均感应电动势与瞬时感应电动势的区别及如何求解.
(2)根据法拉第电磁感应定律、欧姆定律、电流与电量的关系式求解通过导体棒的电荷量.
(3)由E=BLv求出导体棒MN通过圆导轨中心时产生的感应电动势,由闭合电路欧姆定律可求出通过电阻的电流.
解答:解:(1)由法拉第电磁感应定律可得:
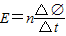 ,
,则有:
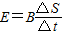
而圆形面积为:△S=πR2
导体棒运动的时间为:
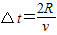
再由闭合电路欧姆定律可得:
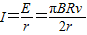
(2)MN从左端到右端的整个过程中,通过r的电荷量:q=It
而闭合电路欧姆定律可得:
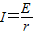
由法拉第电磁感应定律可得:
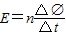
所以q=
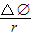 =
=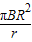
(3)当导体棒MN通过圆导轨中心时,
产生的感应电动势为E=2BRv
由闭合电路欧姆定律可得::
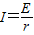
所以通过r的电流:I=2
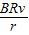
答:(1)在滑动过程中通过电阻r的电流的平均值
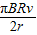 ;
;(2)MN从左端到右端的整个过程中,通过r的电荷量
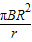 ;
;(3)当MN通过圆导轨中心时,通过r的电流是2
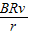 .
.点评:考查法拉第电磁感应定律、闭合电路欧姆定律,且电量与磁通量的变化及电阻有关.并体现了平均感应电动势与瞬时感应电动势的区别及如何求解.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 如图所示,半径为R的光滑半圆轨道竖直放置,两个质量均为m的小球A、B以不同的速率进入轨道,A通过最高点C时,对轨道的压力为3mg,B通过最高点C时,对轨道的压力恰好为零,求:
如图所示,半径为R的光滑半圆轨道竖直放置,两个质量均为m的小球A、B以不同的速率进入轨道,A通过最高点C时,对轨道的压力为3mg,B通过最高点C时,对轨道的压力恰好为零,求: 如图所示,半径为R的vt-sB=l光滑圆弧轨道竖直放置,底端与光滑的水平轨道相接,质量为m的小球B静止光滑水平轨道上,其左侧连接了一轻质弹簧,质量为m的小球A自圆弧轨道的顶端由静止释放,重力加速度为g,小球可视为质点.
如图所示,半径为R的vt-sB=l光滑圆弧轨道竖直放置,底端与光滑的水平轨道相接,质量为m的小球B静止光滑水平轨道上,其左侧连接了一轻质弹簧,质量为m的小球A自圆弧轨道的顶端由静止释放,重力加速度为g,小球可视为质点. 如图所示,半径为R的
如图所示,半径为R的 如图所示,半径为R的半圆轨道BC竖直放置.一个质量为m 的小球以某一初速度从A点出发,经AB段进入半圆轨道,在B点时对轨道的压力为7mg,之后向上运动完成半个圆周运动恰好到达C点.试求:
如图所示,半径为R的半圆轨道BC竖直放置.一个质量为m 的小球以某一初速度从A点出发,经AB段进入半圆轨道,在B点时对轨道的压力为7mg,之后向上运动完成半个圆周运动恰好到达C点.试求: 如图所示,半径为r的圆筒,绕竖直中心轴OO′旋转,小物块a靠在圆筒的内壁上,它与圆筒内壁间的动摩擦因数为μ,现要使a不下落,则圆筒转动的角速度ω至少为( )
如图所示,半径为r的圆筒,绕竖直中心轴OO′旋转,小物块a靠在圆筒的内壁上,它与圆筒内壁间的动摩擦因数为μ,现要使a不下落,则圆筒转动的角速度ω至少为( )