题目内容
已知万有引力常量G、月球中心到地球中心的距离R和月球绕地球运行的周期T，由以上数据，可以计算出（ ）A．月球的质量和月球绕地球运行速度的大小
B．地球的质量和月球绕地球运行速度的大小
C．月球的半径和地球自转的角速度的大小
D．地球的半径和地球自转的角速度的大小
【答案】分析：万有引力的应用之一就是计算中心天体的质量，计算原理就是万有引力提供球绕天体圆周运动的向心力，列式只能计算中心天体的质量．可求出月球绕地球运行速度的大小．
解答：解：月球绕地球做圆周运动，地球对月球的万有引力提供圆周运动的向心力，列式如下：G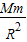
=m
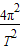R
可得：地球质量M=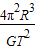
，
月球绕地球运行速度的大小v=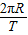
．
根据题中条件求出地球半径和月球半径．故B正确．
故选B
点评：此题中由万有引力提供向心力，根据数据列式可求解中心天体的质量，注意向心力的表达式需跟已知量相一致．
解答：解：月球绕地球做圆周运动，地球对月球的万有引力提供圆周运动的向心力，列式如下：G
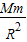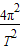=mR可得：地球质量M=
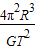，月球绕地球运行速度的大小v=
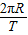．根据题中条件求出地球半径和月球半径．故B正确．
故选B
点评：此题中由万有引力提供向心力，根据数据列式可求解中心天体的质量，注意向心力的表达式需跟已知量相一致．
练习册系列答案
相关题目
太阳系八大行星绕太阳运动的轨道可粗略地认为是圆，各行星的半径、日星距离和质量如下表所示：
|
| A、太阳系的八大行星中，海王星的圆周运动速率最大 |
| B、太阳系的八大行星中，水星的圆周运动周期最大 |
| C、如果已知地球的公转周期为1年，万有引力常量G=6.67×10-11Nm2/kg2，再利用地球和太阳间的距离，则可以求出太阳的质量 |
| D、如果已知万有引力常量G=6.67×10-11Nm2/kg2，并忽略地球的自转，利用地球的半径以及地球表面的重力加g=10m/s2，则可以求出太阳的质量 |