题目内容
一物块以一定的初速度沿斜面向上滑出，利用速度传感器可以在计算机屏幕上得到其速度大小随时间的变化关系图象如图所示，g=10m/s2．求：（1）物块向上滑行的最大距离S；
（2）斜面的倾角θ．
分析：（1）根据速度时间图象得到物体的运动规律，根据平均速度公式列式求解；
（2）从速度时间图象分别得到上滑和下滑的加速度，然后受力分析，根据牛顿第二定律列式求解．
（2）从速度时间图象分别得到上滑和下滑的加速度，然后受力分析，根据牛顿第二定律列式求解．
解答：解：（1）物块向上滑行时做匀加速直线运动，根据平均速度公式，有
x1=
?t1=
?0.5=1m
即物块向上滑行的最大距离S为1m．
（2）物体上滑时受到重力、支持力和摩擦力，此时的加速度为a1=
=
=-8m/s2
根据牛顿第二定律，有-mgsinθ-f=ma1
物体下滑时受到重力、支持力和摩擦力，此时的加速度为a2=
=
=-2m/s2
根据牛顿第二定律，有-mgsinθ+f=ma2
解得
θ=30°
即斜面的倾角为30°．
x1=
. |
| v1 |
| 0+4 |
| 2 |
即物块向上滑行的最大距离S为1m．
（2）物体上滑时受到重力、支持力和摩擦力，此时的加速度为a1=
| △v1 |
| △t1 |
| 0-4 |
| 0.5 |
根据牛顿第二定律，有-mgsinθ-f=ma1
物体下滑时受到重力、支持力和摩擦力，此时的加速度为a2=
| △v2 |
| △t2 |
| -2-0 |
| 1 |
根据牛顿第二定律，有-mgsinθ+f=ma2
解得
θ=30°
即斜面的倾角为30°．
点评：本题关键根据速度时间图象得到物体上滑和下滑的加速度，然后受力分析并根据牛顿第二定律列式求解出斜面的倾角．
练习册系列答案
相关题目
（2011?梧州模拟）一物块以一定的初速度沿斜面向上滑出，利用速度传感器可以在计算机屏幕上得到其速度大小随时间的变化关系图象如图所示，求：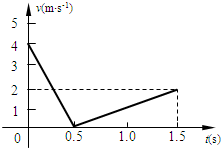
一物块以一定的初速度沿斜面向上滑，利用速度传感器可以在计算机屏幕上得到其速度大小随时间的变化关系如图所示，g=10m/s2．求：
如图甲所示，斜面体固定在水平面上，一物块以一定的初速度v0沿斜面上滑，物块在斜面上整个过程运动的v-t图象如图乙所示．下列说法正确的是（ ）
（A组） 一物块以一定的初速度沿斜面向上滑出，利用DIS实验系统，在计算机屏幕上得到其速度大小随时间的变化关系图象如图所示．求：（g=10m/s2）