题目内容
如图所示,甲车质量m1=m,在车上有质量为M=2m的人,甲车(连同车上的人)从足够长的斜坡上高h处由静止滑下,到水平面上后继续向前滑动,此时质量m2=2m的乙车正以v的速度迎面滑来.已知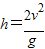 .为了避免两车发生碰撞,当两车相距适当距离时,人从甲车跳上了乙车.试求人跳离甲车的水平速度(相对地面)应满足什么条件?不计地面和斜坡的摩擦,小车和人均可看作质点.
.为了避免两车发生碰撞,当两车相距适当距离时,人从甲车跳上了乙车.试求人跳离甲车的水平速度(相对地面)应满足什么条件?不计地面和斜坡的摩擦,小车和人均可看作质点.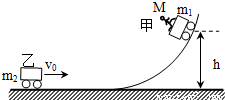
【答案】分析:甲车下滑过程中机械能守恒,由机械能守恒定律可以求出甲滑到水平面时的速度;人从甲车上跳出的过程,人与甲车组成的系统动量守恒,人落到乙车的过程,人与车组成的系统动量守恒,当两车速度相等时,两车可以避免碰撞,由动量守恒定律可以求出人跳出车的速度.
解答:解:设甲车(包括人)滑下斜坡后速度v1,
由机械能守恒定律得:(m1+M)gh= (m1+M)v12,
(m1+M)v12,
已知,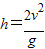 ,解得:v1=2v;
,解得:v1=2v;
设人跳出甲车的水平速度(相对地面)为v.
在人跳离甲车和人跳上乙车过程中各自系统动量守恒,
设人跳离甲车和跳上乙车后,两车的速度分别为v1′和v2′,
由动量守恒定律得:人跳离甲车时:(m1+M)v1=Mv+m1v1′,
人跳上乙车时:Mv-m2v=(M+m2)v2′,
解得:v1′=6v-2v ①,v2′= v-
v- v0 ②,
v0 ②,
两车不可能再发生碰撞的临界条件是:v1′=±v2′,
当v1′=v2′时,由①②解得:v=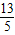 v,
v,
当v1′=-v2′时,由①②解得:v=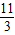 v,
v,
故v的取值范围为: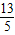 v≤v≤
v≤v≤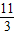 v;
v;
点评:应用动量守恒定律即可正确解题,本题的难点是研究对象的选择与避免碰撞条件的确定.
解答:解:设甲车(包括人)滑下斜坡后速度v1,
由机械能守恒定律得:(m1+M)gh=
 (m1+M)v12,
(m1+M)v12,已知,
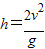 ,解得:v1=2v;
,解得:v1=2v;设人跳出甲车的水平速度(相对地面)为v.
在人跳离甲车和人跳上乙车过程中各自系统动量守恒,
设人跳离甲车和跳上乙车后,两车的速度分别为v1′和v2′,
由动量守恒定律得:人跳离甲车时:(m1+M)v1=Mv+m1v1′,
人跳上乙车时:Mv-m2v=(M+m2)v2′,
解得:v1′=6v-2v ①,v2′=
 v-
v- v0 ②,
v0 ②,两车不可能再发生碰撞的临界条件是:v1′=±v2′,
当v1′=v2′时,由①②解得:v=
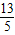 v,
v,当v1′=-v2′时,由①②解得:v=
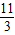 v,
v,故v的取值范围为:
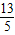 v≤v≤
v≤v≤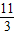 v;
v;点评:应用动量守恒定律即可正确解题,本题的难点是研究对象的选择与避免碰撞条件的确定.

练习册系列答案
相关题目
 (2007?佛山二模)如图所示,甲车质量m1=m,在车上有质量为M=2m的人,甲车(连同车上的人)从足够长的斜坡上高h处由静止滑下,到水平面上后继续向前滑动,此时质量m2=2m的乙车正以v0的速度迎面滑来.已知
(2007?佛山二模)如图所示,甲车质量m1=m,在车上有质量为M=2m的人,甲车(连同车上的人)从足够长的斜坡上高h处由静止滑下,到水平面上后继续向前滑动,此时质量m2=2m的乙车正以v0的速度迎面滑来.已知 如图所示,甲车质量m1=m,在车上有质量为M=2m的人,甲车(连同车上的人)从足够长的斜坡上高处由静止滑下,到水平面上时以水平速度v0向前滑动,此时质量m2=m的乙车正以v0的速度迎面滑来,为了使两车不可能发生碰撞,当两车相距适当距离时,人从甲车跳上乙车,试求人跳离甲车的水平速度(相对地面)应满足什么条件?不计地面和斜坡的摩擦,小车和人均可看作质点.
如图所示,甲车质量m1=m,在车上有质量为M=2m的人,甲车(连同车上的人)从足够长的斜坡上高处由静止滑下,到水平面上时以水平速度v0向前滑动,此时质量m2=m的乙车正以v0的速度迎面滑来,为了使两车不可能发生碰撞,当两车相距适当距离时,人从甲车跳上乙车,试求人跳离甲车的水平速度(相对地面)应满足什么条件?不计地面和斜坡的摩擦,小车和人均可看作质点.
