��Ŀ����
7���ҹ�������̽��ƻ����϶̡�����������ʵʩ����Լ��ʮ������ʱ����ɣ�2007��10��24�գ����϶�һ�š�����̽�����Ƿ���ɹ���������ijͬѧ���й������֪ʶ��Ƶ��������⣬��������1������֪��������ΪM�������Ƶ����˶�������ΪT���Ұ������Ƶ�����˶����ƿ���������Բ���˶���������������ΪG������������Ƶ����˶��Ĺ���뾶r��
��2����ijλ�Ա����·ɴ���½�����������ijˮƽ�����Ϸ�h�ߴ����ٶ�v0ˮƽ�׳�һ��С��С����ص���������ˮƽ����Ϊx����֪����뾶ΪR��������������ΪG����������������M����
���� ��1�����������ܵ�������������������ʽ���뾶��
��2���ȸ���ƽ���˶��˶���֪ʶ������������������ٶȣ��ٸ����������������������������ʽ��⣮
��� �⣺��1������������ΪM������Ĺ���뾶Ϊr����
$\frac{GMm}{r^2}=m{��\frac{2��}{T}��^2}r$
��ã�$r=\root{3}{{\frac{{GM{T^2}}}{4��}}}$
��2�������������������ٶ�Ϊg������ƽ���˶�������ʽ�ã�
x=v0t
$h=\frac{1}{2}g{t^2}$
��ã�$g=\frac{{2h{v_0}^2}}{x^2}$
����$\frac{{G{M_��}m}}{R^2}=mg$
��ã�${M_��}=\frac{{2h{R^2}v_0^2}}{{G{x^2}}}$
�𣺣�1�������Ƶ����˶��Ĺ���뾶rΪ$\root{3}{\frac{GM{T}^{2}}{4��}}$��
��2�������������M��Ϊ$\frac{2h{R}^{2}{v}_{0}^{2}}{G{x}^{2}}$��
���� ����ؼ���Ҫץס������洦���������������������������������ٶȣ�����ƽ���˶���֪ʶ����������ٶȣ��Լ��������ܵ����������ṩ������������ʽ��⣮

��ϰ��ϵ�д�
 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�
�����Ŀ
11�� ��ͼ��ʾ���̶�������ͬһˮƽ���ڵ�����ƽ�г�ֱ��������ļ��Ϊd�����Ҷ˽�����ֵΪR�ĵ��裬����װ�ô�����ֱ���ϵĴŸ�Ӧǿ�ȴ�СΪB����ǿ�ų��У�һ����Ϊm�������ֲ����ȣ��ĵ����ab��ֱ�ڵ�����ã����������챣�����ýӴ������뵼��֮��Ķ�Ħ������Ϊ�̣�������ˮƽ����ֱ�ڸ˵ĺ���F�����´Ӿ�ֹ��ʼ�ص����˶�����lʱ���ٶ�ǡ�ôﵽ����˶������и�ʼ���뵼�챣�ִ�ֱ������˽����·�ĵ���Ϊr��������費�ƣ��������ٶȴ�СΪg����˹��̣�������
��ͼ��ʾ���̶�������ͬһˮƽ���ڵ�����ƽ�г�ֱ��������ļ��Ϊd�����Ҷ˽�����ֵΪR�ĵ��裬����װ�ô�����ֱ���ϵĴŸ�Ӧǿ�ȴ�СΪB����ǿ�ų��У�һ����Ϊm�������ֲ����ȣ��ĵ����ab��ֱ�ڵ�����ã����������챣�����ýӴ������뵼��֮��Ķ�Ħ������Ϊ�̣�������ˮƽ����ֱ�ڸ˵ĺ���F�����´Ӿ�ֹ��ʼ�ص����˶�����lʱ���ٶ�ǡ�ôﵽ����˶������и�ʼ���뵼�챣�ִ�ֱ������˽����·�ĵ���Ϊr��������費�ƣ��������ٶȴ�СΪg����˹��̣�������
 ��ͼ��ʾ���̶�������ͬһˮƽ���ڵ�����ƽ�г�ֱ��������ļ��Ϊd�����Ҷ˽�����ֵΪR�ĵ��裬����װ�ô�����ֱ���ϵĴŸ�Ӧǿ�ȴ�СΪB����ǿ�ų��У�һ����Ϊm�������ֲ����ȣ��ĵ����ab��ֱ�ڵ�����ã����������챣�����ýӴ������뵼��֮��Ķ�Ħ������Ϊ�̣�������ˮƽ����ֱ�ڸ˵ĺ���F�����´Ӿ�ֹ��ʼ�ص����˶�����lʱ���ٶ�ǡ�ôﵽ����˶������и�ʼ���뵼�챣�ִ�ֱ������˽����·�ĵ���Ϊr��������費�ƣ��������ٶȴ�СΪg����˹��̣�������
��ͼ��ʾ���̶�������ͬһˮƽ���ڵ�����ƽ�г�ֱ��������ļ��Ϊd�����Ҷ˽�����ֵΪR�ĵ��裬����װ�ô�����ֱ���ϵĴŸ�Ӧǿ�ȴ�СΪB����ǿ�ų��У�һ����Ϊm�������ֲ����ȣ��ĵ����ab��ֱ�ڵ�����ã����������챣�����ýӴ������뵼��֮��Ķ�Ħ������Ϊ�̣�������ˮƽ����ֱ�ڸ˵ĺ���F�����´Ӿ�ֹ��ʼ�ص����˶�����lʱ���ٶ�ǡ�ôﵽ����˶������и�ʼ���뵼�챣�ִ�ֱ������˽����·�ĵ���Ϊr��������費�ƣ��������ٶȴ�СΪg����˹��̣�������| A�� | �˵��ٶ����ֵΪ$\frac{F-��mgR}{{B}^{2}{d}^{2}}$ | |
| B�� | ��������R�ĵ����Ϊ$\frac{Bdl}{R+r}$ | |
| C�� | ����F���Ĺ���Ħ�������Ĺ�֮�͵��ڸ˶��ܵı仯�� | |
| D�� | ����F���Ĺ��밲�������Ĺ�֮�ʹ��ڸ˶��ܵı仯�� |
18�� ��ͼ��ʾ����ƽ�а�������������Ƶ�ָ��ƫתһ���Ƕȣ������ı���������ĵ��������С�������ľ��룬ͬʱ���������������ʰ壬��ô�����ָ���ƫת�Ƕȣ�������
��ͼ��ʾ����ƽ�а�������������Ƶ�ָ��ƫתһ���Ƕȣ������ı���������ĵ��������С�������ľ��룬ͬʱ���������������ʰ壬��ô�����ָ���ƫת�Ƕȣ�������
 ��ͼ��ʾ����ƽ�а�������������Ƶ�ָ��ƫתһ���Ƕȣ������ı���������ĵ��������С�������ľ��룬ͬʱ���������������ʰ壬��ô�����ָ���ƫת�Ƕȣ�������
��ͼ��ʾ����ƽ�а�������������Ƶ�ָ��ƫתһ���Ƕȣ������ı���������ĵ��������С�������ľ��룬ͬʱ���������������ʰ壬��ô�����ָ���ƫת�Ƕȣ�������| A�� | һ������ | B�� | һ����С | C�� | һ������ | D�� | ��ȷ�� |
12��������Ԫ��${\;}_{90}^{234}$Th��˥�䷽��Ϊ${\;}_{90}^{234}$Th��${\;}_{91}^{234}$Pa+X�����б�����ȷ���ǣ�������
| A�� | X����Thԭ���ͷŵĺ������ | B�� | ��˥���Ǧ�˥�� | ||
| C�� | ����ѹ�������˥��ø��� | D�� | Th����˥��ʱԭ�Ӻ�Ҫ�������� |
19�� ����ѡ����������ѧ��������ͨ���о�ƽ�а�����������Ĵ����͵Σ��Ƚ�ȷ�زⶨ�˵��ӵĵ��������ͼ��ʾ��ƽ�а������������M��N���Ϊd��������ֱ����ѹΪU�ĺ㶨��Դ�������ӣ�����M�����磮����һ����Ϊm�Ĵ����͵��ڼ������봦�ھ�ֹ״̬���Ҵ�ʱ�������������͵δ�������ı�ֵΪk��������
����ѡ����������ѧ��������ͨ���о�ƽ�а�����������Ĵ����͵Σ��Ƚ�ȷ�زⶨ�˵��ӵĵ��������ͼ��ʾ��ƽ�а������������M��N���Ϊd��������ֱ����ѹΪU�ĺ㶨��Դ�������ӣ�����M�����磮����һ����Ϊm�Ĵ����͵��ڼ������봦�ھ�ֹ״̬���Ҵ�ʱ�������������͵δ�������ı�ֵΪk��������
 ����ѡ����������ѧ��������ͨ���о�ƽ�а�����������Ĵ����͵Σ��Ƚ�ȷ�زⶨ�˵��ӵĵ��������ͼ��ʾ��ƽ�а������������M��N���Ϊd��������ֱ����ѹΪU�ĺ㶨��Դ�������ӣ�����M�����磮����һ����Ϊm�Ĵ����͵��ڼ������봦�ھ�ֹ״̬���Ҵ�ʱ�������������͵δ�������ı�ֵΪk��������
����ѡ����������ѧ��������ͨ���о�ƽ�а�����������Ĵ����͵Σ��Ƚ�ȷ�زⶨ�˵��ӵĵ��������ͼ��ʾ��ƽ�а������������M��N���Ϊd��������ֱ����ѹΪU�ĺ㶨��Դ�������ӣ�����M�����磮����һ����Ϊm�Ĵ����͵��ڼ������봦�ھ�ֹ״̬���Ҵ�ʱ�������������͵δ�������ı�ֵΪk��������| A�� | �͵δ����� | |
| B�� | �͵δ������Ϊ$\frac{mg}{Ud}$ | |
| C�� | �������ĵ���Ϊ$\frac{kmgd}{{U}^{2}}$ | |
| D�� | ������N���»����ƶ�һС�ξ��룬�͵ν������˶� |
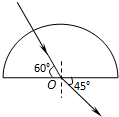 ��ͼ��ʾ��һ����ɫ�������Բ����ש��Բ��O�����������ױߵļн�Ϊ60�㣬���������ױߵļн�Ϊ45�㣬��֪����й���Ϊc�����������ڲ���ש�еĴ����ٶ�v��
��ͼ��ʾ��һ����ɫ�������Բ����ש��Բ��O�����������ױߵļн�Ϊ60�㣬���������ױߵļн�Ϊ45�㣬��֪����й���Ϊc�����������ڲ���ש�еĴ����ٶ�v�� ��ͼ��ʾ������Ϊ1kg�����壬��ijһ���ٶ�v����A�������ع⻬�Ĺ���˶���Բ����뾶ΪR=10m�����ƿ���������������ͨ��B��ʱ���ٶ�Ϊ30m/s����
��ͼ��ʾ������Ϊ1kg�����壬��ijһ���ٶ�v����A�������ع⻬�Ĺ���˶���Բ����뾶ΪR=10m�����ƿ���������������ͨ��B��ʱ���ٶ�Ϊ30m/s���� ��ͼ��ʾ���̶���O��ϵһ��L=0.6m��ϸ����ϸ�����¶�ϵһ����m=1.0kg��С����Ϊ�ʵ㣩��ԭ�����ھ�ֹ״̬������ƽ̨��B��Ӵ�����ƽ̨��ѹ����ƽ̨��h=0.80m��һ����M=2.0kg����鿪ʼ��ֹ��ƽ̨�ϵ�P�㣬�ֶ�Mʩ��һˮƽ���ҵij��ٶ�V0�����M�شֲ�ƽ̨���������˶���ƽ̨��ԵB����С��m��������������С��m������Լ������Բ���˶�������ߵ�Aʱ�����ϵ�����ǡ�õ��ڰ������������M����ˮƽ�����ϵ�C�㣬��ˮƽλ��S=1.2m�����ƿ���������g=10m/s2����
��ͼ��ʾ���̶���O��ϵһ��L=0.6m��ϸ����ϸ�����¶�ϵһ����m=1.0kg��С����Ϊ�ʵ㣩��ԭ�����ھ�ֹ״̬������ƽ̨��B��Ӵ�����ƽ̨��ѹ����ƽ̨��h=0.80m��һ����M=2.0kg����鿪ʼ��ֹ��ƽ̨�ϵ�P�㣬�ֶ�Mʩ��һˮƽ���ҵij��ٶ�V0�����M�شֲ�ƽ̨���������˶���ƽ̨��ԵB����С��m��������������С��m������Լ������Բ���˶�������ߵ�Aʱ�����ϵ�����ǡ�õ��ڰ������������M����ˮƽ�����ϵ�C�㣬��ˮƽλ��S=1.2m�����ƿ���������g=10m/s2����