题目内容

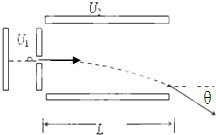精英家教网如图所示，一个初速度为零的带电粒子经电压U1的加速电场加速后，沿垂直于偏转电场的场强方向进入偏转电场．已知偏转电场两平行板间的电势差为U2，极板长为L，两板间的距离为d，带电粒子通过偏转电场时的偏转角为θ．试证明：tanθ=
U2 L2U 1 d
．
分析：由粒子在电场中加速与偏转，根据动能定理，结合运动学公式，并由运动的合成与分解，与三角函数知识，即可证明．
解答：证明：设带电粒子离开加速电场时的速度为v0，由动能定理得
 qU1=
1
2
m
v
2
0
     ①
带电粒子进人偏转电场后，在电场力作用下做匀变速曲线运动其中平行于极板方向做匀速直线运动，垂直于极板方向做匀加速直线运动
即：L=v0t             ②
vy=at=
qU2
md
t     ③
由②③得：vy=
qU2
md
?
L
v0
          ④
带电粒子通过偏转电场时的偏转角正切值：
  tanθ=
vy
v0
=
qU2L
md
v
2
0
=
U2L
2U1d
    
精英家教网
答：证明如上所示．
点评：考查粒子的加速与偏转，掌握动能定理与牛顿第二定律及运动学公式的应用，注意曲线运动的处理方法与三角函数的正确使用．
练习册系列答案
相关题目
如图所示，一个初速度为零的带正电的粒子经过MN两平行板间电场加速后，从N板上的孔射出，当带电粒子到达P点时，长方形abcd的区域内开始加一大小不变、方向垂直于纸面且方向交替变化的匀强磁场，磁感应强度B=0.4T．每经过t=
π
4
×10-3s，磁场方向变化一次，且当粒子到达P点时磁场的方向指向纸外．在Q处有一静止的中性粒子，PQ间距离s=3.0m，PQ直线垂直平分ab、cd．已知长方形abcd区域的宽度D=1.6m，带电粒子的荷质比
q
m
=1.0×104C/kg，不计重力．
（1）试通过计算说明，当加速电压为U=200V时，带电粒子能否与中性粒子碰撞？
（2）要使该带电粒子能与位于Q处的中性粒子的碰撞，试求加速电压的最大值Umax．
如图所示，一个初速度为零的带正电粒子从M板开始运动，经过MN两平行板间的电场加速后，从N板上的小孔射入长方形区域abcd.当带电粒子到达P点时，长方形区域内出现大小不变、方向垂直于纸面且方向交替变化的匀强磁场，磁感应强度B=0.4 T，每经过t=×10-3 s磁场方向变化一次，粒子到达P点时磁场方向恰指向纸外，在Q处有一个静止的中性粒子，P、Q间距离PQ=3.0 m，直线PQ垂直平分ab、cd.已知c、d相距D=1.5 m，带电粒子的比荷=1.0×104 C/kg，重力不计，求：

(1)如果加速电压U=200 V，带电粒子能否与中性粒子碰撞?

(2)能使带电粒子与中性粒子碰撞，加速电压的最大值是多少.
如图所示，一个初速度为零的带正电的粒子经过M、N两平行板间电场加速后，从N板上的孔射出，当带电粒子到达P点时，长方形ABCD区域内出现大小不变、方向垂直于纸面且更替变化的匀强磁场，磁感应强度B=0.4 T，每经过t=×10-3 s，磁场方向变化一次.粒子到达P点时出现的磁场方向指向纸外，在Q处有一静止的中性粒子，P、Q间的距离s=3.0 m,PQ直线垂直平分AB、CD.已知d=1.6 m，带电粒子的比荷为1.0×104 C/kg，不计重力.求：

（1）加速电压为200 V时带电粒子能否与中性粒子碰撞？

（2）画出其轨迹；

（3）要使带电粒子与中性粒子碰撞，加速电压的最大值为多大？
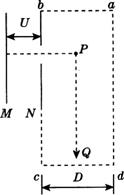
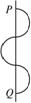
如图所示，一个初速度为零的带正电的粒子经过MN两平行板间电场加速后，从N板上的孔射出，当带电粒子到达P点时，长方形abcd的区域内开始加一大小不变、方向垂直于纸面且方向交替变化的匀强磁场，磁感应强度B=0.4T．每经过s，磁场方向变化一次，且当粒子到达P点时磁场的方向指向纸外．在Q处有一静止的中性粒子，PQ间距离s=3.0m，PQ直线垂直平分ab、cd．已知长方形abcd区域的宽度D=1.6m，带电粒子的荷质比=1.0×104C/kg，不计重力．
（1）试通过计算说明，当加速电压为U=200V时，带电粒子能否与中性粒子碰撞？
（2）要使该带电粒子能与位于Q处的中性粒子的碰撞，试求加速电压的最大值Umax．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网