题目内容
6. 如图所示,遥控电动赛车(可视为质点)从A点由静止出发,经过时间t后关闭电动机,赛车继续前进至B点后进入固定的圆形光滑过山车轨道,通过轨道最高点P后又进入水平轨道CD上.已知赛车在水平轨道AB部分和CD部分运动时受到的阻力恒为车重的0.5倍,赛车的质量m=0.4kg,通电后赛车的电动机以额定功率P=2W工作,轨道AB的长度L=2m,圆形轨道的半径R=0.5m,空气阻力可以忽略,取重力加速度g=10m/s2.某次比赛,要求赛车在运动过程中既不能脱离轨道,又要在CD轨道上运动的路程最短.在此条件下,求:
如图所示,遥控电动赛车(可视为质点)从A点由静止出发,经过时间t后关闭电动机,赛车继续前进至B点后进入固定的圆形光滑过山车轨道,通过轨道最高点P后又进入水平轨道CD上.已知赛车在水平轨道AB部分和CD部分运动时受到的阻力恒为车重的0.5倍,赛车的质量m=0.4kg,通电后赛车的电动机以额定功率P=2W工作,轨道AB的长度L=2m,圆形轨道的半径R=0.5m,空气阻力可以忽略,取重力加速度g=10m/s2.某次比赛,要求赛车在运动过程中既不能脱离轨道,又要在CD轨道上运动的路程最短.在此条件下,求:(1)赛车过P点时,不脱离轨道的最小速度Vp;
(2)赛车在CD轨道上运动的最短路程x;
(3)赛车电动机工作的时间t.
分析 (1)赛车在电动机牵引力作用下从静止开始加速运动,之后关闭发动机滑行,正好能在运动过程中既不能脱离轨道,又在CD轨道上运动的路程最短.因此利用车恰能通过轨道最高来求出P点速度;
(2)(3)根据机械能守恒定律,求出进入轨道C点的最小速度,从而由动能定理来求出CD轨道上运动的最短路程,同时再由动能定理来求出赛车电动机工作的时间.
解答 解:(1)要求赛车在运动过程中既不能脱离轨道,又在CD轨道上运动的路程最短,则赛车经过圆轨道P点时速度最小,此时赛车对轨道的压力为零,重力提供向心力:
mg=m$\frac{{V}_{p}}{R}$
Vp=$\sqrt{gR}$=$\sqrt{10×0.5}$=$\sqrt{5}$m/s
(2)赛车在C点的速度为vC,由机械能守恒定律可得:
mg•2R+$\frac{1}{2}$mV${\;}_{P}^{2}$=$\frac{1}{2}$mV${\;}_{c}^{2}$
由上述两式联立,代入数据可得:
vC=5 m/s
设赛车在CD轨道上运动的最短路程为x,由动能定理可得:-kmgx=0-$\frac{1}{2}$mV${\;}_{C}^{2}$
代入数据可得:x=2.5 m
(3)由于竖直圆轨道光滑,由机械能守恒定律可知:
vB=vC=5 m/s
从A点到B点的运动过程中,由能量守恒定律可得:
Pt=kmgL+$\frac{1}{2}$mV${\;}_{B}^{2}$
代入数据可得:t=4.5 s
答:(1)赛车过P点时,不脱离轨道的最小速度Vp为$\sqrt{5}$m/s;
(2)赛车在CD轨道上运动的最短路程x为2.5m;
(3)赛车电动机工作的时间t为4.5s.
点评 本题突破口是小车恰能通过最高点时,就是小车在CD轨道上运动的最短路程.同时对动能定理,机械能守恒定律理解.

 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案 如图是蹦床运动员落在弹簧床面的示意图,在弹簧弹力的作用下,运动员有一段竖直向下做减速运动的缓冲过程,忽略空气阻力,在此过程中( )
如图是蹦床运动员落在弹簧床面的示意图,在弹簧弹力的作用下,运动员有一段竖直向下做减速运动的缓冲过程,忽略空气阻力,在此过程中( )| A. | 运动员处于失重状态 | |
| B. | 运动员所受合外力方向竖直向上 | |
| C. | 运动员对弹簧床压力大于弹簧床对运动员支持力 | |
| D. | 运动员的机械能减少了 |
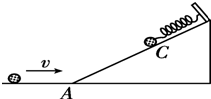 如图所示,光滑斜面的顶端固定一弹簧,一小球向右滑行,并冲上固定在地面上的斜面.设小球在斜面最低点A的速度为V,压缩弹簧至C点时弹簧最短,C点距地面高度为h,则从A到C的过程中弹簧弹性势能的增加量是( )
如图所示,光滑斜面的顶端固定一弹簧,一小球向右滑行,并冲上固定在地面上的斜面.设小球在斜面最低点A的速度为V,压缩弹簧至C点时弹簧最短,C点距地面高度为h,则从A到C的过程中弹簧弹性势能的增加量是( )| A. | mgh-$\frac{1}{2}$mv2 | B. | $\frac{1}{2}$mv2-mgh | C. | -mgh | D. | -[mgh+$\frac{1}{2}$mv2] |
 如图所示,A、B、C是在地球大气层外圆形轨道上运动的3颗卫星,已知mA=mB>mC,下列说法正确的是( )
如图所示,A、B、C是在地球大气层外圆形轨道上运动的3颗卫星,已知mA=mB>mC,下列说法正确的是( )| A. | 角速度大小的关系是ωA>ωB=ωC | B. | 周期关系是TA>TB=TC | ||
| C. | 向心力大小的关系是FA=FB>FC | D. | 向心加速度大小的关系是aA<aB=aC |

(1)打图1中D点时重物的速度vD=3.56m/s( 保留三位有效数字),并在图2坐标纸上作出其v-t图象.
(2)由上述图象知,重物下落过程的加速度明显小于当地的重力加速度,表明重物下落过程中机械能减少(选填“增加”、“守恒”或“减少”),并分析形成这一结论的原因.
| 计数点 | A | B | C | D | E |
| 速度v/(m﹒s-1) | 0.96 | 1.91 | 2.86 | 4.27 |

| A. | 从0到t1时间内,导线框中电流的方向为abcda | |
| B. | 从0到t1时间内,导线框中电流越来越小 | |
| C. | 从0到t2时间内,导线框中电流的方向始终为adcba | |
| D. | 从0到t2时间内,导线框ab边受到的安培力越来越大 |

 某实验小组在进行“用单摆测定重力加速度”的实验中,已知单摆在摆动过程中的摆角小于5,在测量单摆的周期时,从单摆运动到最低点开始计时且记数为0,到第n次经过最低点所用的时间为t,在测量单摆的摆长时,先用毫米刻度尺测得摆球悬挂后的摆线长(从悬点到摆球的最上端)为L′,再用游标卡尺测得摆球的直径为d(读数如图).
某实验小组在进行“用单摆测定重力加速度”的实验中,已知单摆在摆动过程中的摆角小于5,在测量单摆的周期时,从单摆运动到最低点开始计时且记数为0,到第n次经过最低点所用的时间为t,在测量单摆的摆长时,先用毫米刻度尺测得摆球悬挂后的摆线长(从悬点到摆球的最上端)为L′,再用游标卡尺测得摆球的直径为d(读数如图).