题目内容
如图所示，粗细均匀的玻璃细管上端封闭，下端开口，竖直插在大而深的水银槽中，管内封闭有一定质量的空气，玻璃细管足够长，管内气柱长4cm，管内外水银面高度差为10cm．现将玻璃管沿竖直方向缓慢移动．（大气压强相当于75cmHg）求：（1）若要使管内外水银面恰好相平，此时管内气柱的长度；
（2）若要使管内外水银面高度差为15cm，玻璃管又应如何移动多少距离．
分析：（1）确定好两个状态下的状态参量，由玻意耳定律求解；
（2）确定好两个状态下的状态参量，由玻意耳定律求解空气柱长度，再根据几何关系求解；
（2）确定好两个状态下的状态参量，由玻意耳定律求解空气柱长度，再根据几何关系求解；
解答：解：（1）设玻璃管的横截面为S1，玻璃管向上移动为等温变化，
初态：P1=65cmHg，V1=4S1 末态：P2=75cmHg V2=l2S1
由玻恴耳定律：P1V1=P2V2 得：l2=
=
cm=3.5cm
（2）使管内外水银面高度差为15cm，此时封闭气体压强 P3=P0-15=75-15cmHg=60cmHg
V3=l3S1
由玻恴耳定律：P1V1=P3V3 得：l3=
=
cm=4.33cm
即玻璃管应向上移动△h=15-10+（4.33-4）cm=5.33cm
答：（1）管内气柱的长度为3.5cm，
（2）要使管内外水银面高度差为15cm，玻璃管应向上移动5.33cm距离．
初态：P1=65cmHg，V1=4S1 末态：P2=75cmHg V2=l2S1
由玻恴耳定律：P1V1=P2V2 得：l2=
| P1V1 |
| P2 |
| 65×4 |
| 75 |
（2）使管内外水银面高度差为15cm，此时封闭气体压强 P3=P0-15=75-15cmHg=60cmHg
V3=l3S1
由玻恴耳定律：P1V1=P3V3 得：l3=
| P1V1 |
| P2 |
| 65×4 |
| 60 |
即玻璃管应向上移动△h=15-10+（4.33-4）cm=5.33cm
答：（1）管内气柱的长度为3.5cm，
（2）要使管内外水银面高度差为15cm，玻璃管应向上移动5.33cm距离．
点评：查玻意耳定律的应用，会确定初末状态的参量是解题的关键．
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南大学出版社系列答案
相关题目
如图所示，粗细均匀的玻璃管，当温度为27℃时，封闭在管内的空气柱AB长为30cm，BC长为10cm，管内水银柱水平部分CD长为18cm，竖直部分DE长为15cm，外界大气压强为75cmHg，问：要使水平管内没有水银柱，温度至少要升高到多少℃？
（2012?长宁区一模）如图所示，粗细均匀的U形管竖直放置，左端封闭，右端开口，左端用水银封闭着长L=10cm的理想气体，当温度为27℃时，两管水银面的高度差△h=2cm．设外界大气压为1.0×105Pa（即75cmHg）．为了使左、右两管中的水银面相平，求：
（2011?上海二模）如图所示，粗细均匀的U形管，左端封闭，右端开口，左端用水银封闭着长L=15cm的理想气体，当温度为27℃时，两管水银面的高度差△h=3cm．设外界大气压为1.0×105Pa（即75cmHg）．则：
[物理--选修3-3]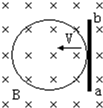
如图所示．粗细均匀的电阻为r的金属圆环放在磁感应强度为B的垂直环面的匀强磁场中，圆环的直径为d．长为d、电阻为