题目内容
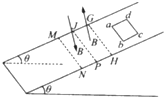
如图所示，在倾角为30°的光滑斜面上固定一光滑金属导轨CDEFG，图中OH∥CD∥FG，∠DEF=60°，CD=DE=EF=FG=OE=L；一根质量为m、长度为2L的导体棒AB在电机牵引下，以恒定速度v0沿OH方向从斜面底端滑上导轨并到达斜面顶端，O是AB棒的中点，AB⊥OH．金属导轨的CD、FG段电阻不计，DEF段与AB棒材料与横截面积均相同，单位长度的电阻均为r，整个斜面处在垂直斜面向上、磁感应强度为B的匀强磁场中．求：
（1）导体棒在导轨DEF上滑动时电路中电流的大小；
（2）导体棒运动到DF位置时AB两端的电压；
（3）将导体棒从底端拉到斜面顶端过程电机对杆做的功．
（1）导体棒在导轨DEF上滑动时电路中电流的大小；
（2）导体棒运动到DF位置时AB两端的电压；
（3）将导体棒从底端拉到斜面顶端过程电机对杆做的功．
（1）设AB棒等效切割长度为l，则
感应电动势为E=Blv0
回路电阻为R=3lr
回路电流为I=
| E |
| R |
| Bv0 |
| 3r |
（2）AB棒滑到DF处时
AB两端的电压UBA=UDA+UFD+UBF
UDA+UBF=BLv0
而UDF=
| 2lr |
| 3lr |
| 2 |
| 3 |
得UBA=UDA+UFD+UBF=
| 5 |
| 3 |
（3）导体棒重力势能的增加量△EP=mg（2L+Lcos30°）sin30°=
4+
| ||
| 4 |
AB棒在DEF上滑动时产生的电热Q1，数值上等于克服安培力做的功Q1=W安
又因为F安∝S，如图，故 Q1=W安=
| 0+F安max |
| 2 |
| ||
| 2 |
| ||
| 12r |
AB棒在CDFG导轨上滑动时产生的电热Q2，电流恒定，电阻不变
则Q2=I2Rt=（
| Bv0 |
| 3r |
| L |
| v0 |
| B2L2v0 |
| 3r |
得，电机做的功W=△EP+Q1+Q2=
4+
| ||
| 4 |
| B2L2v0 |
| 3r |
答：（1）导体棒在导轨DEF上滑动时电路中电流的大小为流为
| Bv0 |
| 3r |
（2）导体棒运动到DF位置时AB两端的电压为
| 5 |
| 3 |
（3）将导体棒从底端拉到斜面顶端过程电机对杆做的功是
4+
| ||
| 4 |
| B2L2v0 |
| 3r |
练习册系列答案
相关题目
如图所示，在倾角为θ=30°的斜面上，固定一宽L=0.25m的平行金属导轨，在导轨上端接入电源和变阻器．电源电动势E=12V，内阻r=1.0Ω一质量m=20g的金属棒ab与两导轨垂直并接触良好．整个装置处于磁感强度B=0.80T、垂直于斜面向上的匀强磁场中（导轨与金属棒的电阻不计）．金属导轨是光滑的，取g=10m/s2，要保持金属棒在导轨上静止，求：
如图所示，在倾角为θ的光滑固定斜面上，劲度系数分别为k1、k2的两个轻弹簧平行于斜面悬挂着，k1在上 k2在下，两弹簧之间有一质量为m1的重物，现用力F（未知）沿斜面向上缓慢推动m2，当两弹簧的总长等于两弹簧的原长之和时，
如图所示，在倾角为30°的斜面上，放置两条宽L=0.5m的平行导轨，将电源、滑动变阻器用导线连接在导轨上，在导轨上横放一根质量m=0.2kg的金属杆ab，电源电动势E=12V，内阻r=0.3Ω，金属杆与导轨间最大静摩擦力为fm=0.6N，磁场方向垂直轨道所在平面，B=0.8T．金属杆ab的电阻为0.2Ω，导轨电阻不计．欲使杆的轨道上保持静止，滑动变阻器的电阻的取值范围多大？（g取10m/s2）
如图所示，在倾角为30°的斜面上，由A点水平抛出一个物体，落在斜面上的B点处，A与B两点间距离是10m，（ 取g=10m/s2）求：
如图所示，在倾角为θ的光滑斜面上，存在着两个大小相等、方向相反的匀强磁场，磁场方向与斜面垂直，两磁场的宽度MJ和JG均为L，一个质量为m、电阻为R、边长也为L的正方形导线框，由静止开始沿斜面下滑，当ab边刚越过GH进入磁场时，线框恰好以速度v0做匀速直线运动；当ab边下滑到JP与MN的中间位置时，线框又恰好以速度v做匀速直线运动．则下列说法正确的是（ ）| A、v=v0 | ||
| B、线框离开MN的过程中电流方向为adcba | ||
| C、当ab边刚越过JP时，线框加速度的大小为3 gsinθ | ||
D、从ab边刚越过GH到ab边刚越过MN过程中，线框产生的热量为2mgLsinθ+
|