题目内容
4. 如图所示,一质量为M=3.0kg的玩具小车在光滑水平轨道上以v0=2.0m/s的速度向右运动,一股水流以u=2.4m/s的水平速度自右向左射向小车左壁,并沿左壁流入车箱内,水的流量为b=0.4kg/s.
如图所示,一质量为M=3.0kg的玩具小车在光滑水平轨道上以v0=2.0m/s的速度向右运动,一股水流以u=2.4m/s的水平速度自右向左射向小车左壁,并沿左壁流入车箱内,水的流量为b=0.4kg/s.(ⅰ)要改变小车的运动方向,射到小车里的水的质量至少是多少?
(ⅱ)当射入小车的水的质量为m0=1.0kg时,小车的速度和加速度各是多大?
分析 (1)要使小车的速度反向,则小车至少应速度减小到零;由动量守恒可求得水的质量;
(2)当车中水的质量为m0=1.0kg时,小车的速度设为v,由动量守恒定律求出小车的速度,在对小车与水整体应用牛顿第二定律列式,对质量为△m的水,由动量定理列式,联立方程即可求解.
解答 解:
(ⅰ)当车速为0时,设水的质量为m,以水平向右为正方向,由动量守恒定律:
Mv0-mu=0
解得:m=2.5kg
(ⅱ)当车中水的质量为m0=1.0kg时,小车的速度设为v,由动量守恒定律:
Mv0-m0u=(M+m0)v
解得:v=0.9m/s
此时,小车与水的总质量为M+m0,由牛顿第二定律:F=(M+m0)a
对质量为△m的水,由动量定理:F△t=△m(v+u)
联立解得:a=0.33m/s2
答:(ⅰ)要改变小车的运动方向,射到小车里的水的质量至少是2.5kg;
(ⅱ)当射入小车的水的质量为m0=1.0kg时,小车的速度和加速度分别为0.9m/s,0.33m/s2.
点评 本题主要考查了动量守恒定律、动量定理以及牛顿第二定律的直接应用,注意在题意中要找出正确的研究对象,再利用动量守恒求解,难度适中.

练习册系列答案
相关题目
9.已知氘核的平均结合能是1.09MeV,氚核的平均结合能是2.78MeV,氦核的平均结合能是7.03MeV.在某次核反应中,1个氘核和1个氚核结合生成1个氦核并放出17.6MeV的能量,下列说法正确的是( )
| A. | 这是一个裂变反应 | |
| B. | 核反应方程式为${\;}_{1}^{2}$H+${\;}_{1}^{3}$H→${\;}_{2}^{4}$He+${\;}_{0}^{1}$n | |
| C. | 目前核电站都采用上述核反应发电 | |
| D. | 该核反应不会有质量亏损 |
10. 如图,质量为m的足球以速度为V0离开桌面,桌面离地面高度为H,当它经过离地面高度为h时,若以桌面为参考面且不计空气阻力,则足球( )
如图,质量为m的足球以速度为V0离开桌面,桌面离地面高度为H,当它经过离地面高度为h时,若以桌面为参考面且不计空气阻力,则足球( )
 如图,质量为m的足球以速度为V0离开桌面,桌面离地面高度为H,当它经过离地面高度为h时,若以桌面为参考面且不计空气阻力,则足球( )
如图,质量为m的足球以速度为V0离开桌面,桌面离地面高度为H,当它经过离地面高度为h时,若以桌面为参考面且不计空气阻力,则足球( )| A. | 机械能$\frac{1}{2}$mV02 | B. | 机械能为$\frac{1}{2}$mV02+mgH | ||
| C. | 动能为$\frac{1}{2}$mV02+mg(H-h) | D. | 动能为mg(H-h) |
19.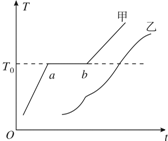 固体甲和固体乙在一定压强下的熔解曲线如图所示,横轴表示时间t,纵轴表示温度T.下列判断正确的有 ( )
固体甲和固体乙在一定压强下的熔解曲线如图所示,横轴表示时间t,纵轴表示温度T.下列判断正确的有 ( )
 固体甲和固体乙在一定压强下的熔解曲线如图所示,横轴表示时间t,纵轴表示温度T.下列判断正确的有 ( )
固体甲和固体乙在一定压强下的熔解曲线如图所示,横轴表示时间t,纵轴表示温度T.下列判断正确的有 ( )| A. | 固体甲一定是晶体,固体乙一定是非晶体 | |
| B. | 固体甲不一定有确定的几何外形,固体乙一定没有确定的几何外形 | |
| C. | 在热传导方面固体甲一定表现出各向异性,固体乙一定表现出各向同性 | |
| D. | 固体甲和固体乙的化学成分有可能相同 | |
| E. | 图线甲中ab段温度不变,所以甲的内能不变 |
9. 如图所示,两个固定的相同细圆环相距一定的距离,同轴平行放置,O1、O2分别为两环的圆心,两环分别带有均匀分布的等量异种电荷,一带正电的粒子从很远处沿轴线飞来并穿过两环,则( )
如图所示,两个固定的相同细圆环相距一定的距离,同轴平行放置,O1、O2分别为两环的圆心,两环分别带有均匀分布的等量异种电荷,一带正电的粒子从很远处沿轴线飞来并穿过两环,则( )
 如图所示,两个固定的相同细圆环相距一定的距离,同轴平行放置,O1、O2分别为两环的圆心,两环分别带有均匀分布的等量异种电荷,一带正电的粒子从很远处沿轴线飞来并穿过两环,则( )
如图所示,两个固定的相同细圆环相距一定的距离,同轴平行放置,O1、O2分别为两环的圆心,两环分别带有均匀分布的等量异种电荷,一带正电的粒子从很远处沿轴线飞来并穿过两环,则( )| A. | 带电粒子在O1和O2点加速大小相等,方向向反 | |
| B. | 带电粒子从O1运动到O2,电势能一直增加 | |
| C. | 带电粒子在O1和O2连线中点动能最小 | |
| D. | 轴线上O1点右侧,O2点左侧都存在场强为零的点,它们关于O1、O2连线中点对称 |
 一束光线以入射角α=60°射入折射率为$\sqrt{3}$、宽度为d0=5cm的玻璃砖,另一完全相同玻璃砖平行放置,相距d=5cm,请画出光路图并求解光线的侧移距离.
一束光线以入射角α=60°射入折射率为$\sqrt{3}$、宽度为d0=5cm的玻璃砖,另一完全相同玻璃砖平行放置,相距d=5cm,请画出光路图并求解光线的侧移距离. 一列简谐横波由O点沿x轴正向传播如图所示,经时间t=6.0×10-2s振动从O点传播到A点,OA两点间的距离为3m.当这列波进入AB区域时,它的传播速度变为原来的3倍,则这列波在OA区域内的频率为25Hz,在AB区域内的波长为6m.
一列简谐横波由O点沿x轴正向传播如图所示,经时间t=6.0×10-2s振动从O点传播到A点,OA两点间的距离为3m.当这列波进入AB区域时,它的传播速度变为原来的3倍,则这列波在OA区域内的频率为25Hz,在AB区域内的波长为6m. 如图甲所示,圆形的刚性金属线圈与一平行板电容器连接,线圈内存在垂直于线圈平面的匀强磁场,取垂直于纸面向里为磁感应强度B的正方向,B随时间t的变化关系如图乙所示.t=0时刻,在平行板电容器间,由静止释放一带正电的粒子(重力可忽略不计),假设粒子运动未碰到极板,不计线圈内部磁场变化对外部空间的影响,下列关于粒子在板间运动的速度图象和位移图象(以向上为正方向)正确的是( )
如图甲所示,圆形的刚性金属线圈与一平行板电容器连接,线圈内存在垂直于线圈平面的匀强磁场,取垂直于纸面向里为磁感应强度B的正方向,B随时间t的变化关系如图乙所示.t=0时刻,在平行板电容器间,由静止释放一带正电的粒子(重力可忽略不计),假设粒子运动未碰到极板,不计线圈内部磁场变化对外部空间的影响,下列关于粒子在板间运动的速度图象和位移图象(以向上为正方向)正确的是( )