��Ŀ����
5�� ��ͼ��ʾ��һ�ڱڹ⻬�����̶���ˮƽ�����ϣ��ھ����ײ�L=54cm����һ�̶��������ϵĿ��������������ײ�֮������һ���������������壬������ͼʾλ��ʱ���������¶�t1=267�棬ѹǿp1=1.5atm�������ѹǿ��0��Ϊ1atm���������������ã����ƻ����ĺ�ȣ��������������ȣ��������ջ����Ƶ�ijһλ�ö�ƽ�⣮��
��ͼ��ʾ��һ�ڱڹ⻬�����̶���ˮƽ�����ϣ��ھ����ײ�L=54cm����һ�̶��������ϵĿ��������������ײ�֮������һ���������������壬������ͼʾλ��ʱ���������¶�t1=267�棬ѹǿp1=1.5atm�������ѹǿ��0��Ϊ1atm���������������ã����ƻ����ĺ�ȣ��������������ȣ��������ջ����Ƶ�ijһλ�ö�ƽ�⣮���ٻ�����Ҫ�뿪������ʱ���������¶ȣ�
�ڷ�������¶��½���t3=27��ʱ���������ײ�֮��ľ��룮
���� �ٻ�����Ҫ�뿪������ǰ���������ݱ仯�����ݲ���������ʽ��⣻
�ڻ����뿪����������ѹ�仯�����ݸ������˶�����ʽ��⣮
��� �⣺�ٻ�����Ҫ�뿪������֮ǰ
��̬��P1=1.5atm T1=267+273K=540K
ĩ̬��P2=P0=1atm
�˹��̵��ݱ仯���ɲ������ɵã�$\frac{{P}_{1}}{{T}_{1}}=\frac{{P}_{2}}{{T}_{2}}$
�������ݽ�ã�${T}_{2}=\frac{{P}_{2}{T}_{1}}{{P}_{1}}=\frac{1��540}{1.5}K=360K$
��t2=T2-273=��360-273����=87��
�ڻ����뿪����������ѹ�仯��
���ݸ������˶��ɵã�$\frac{{L}_{2}S}{{T}_{2}}=\frac{{L}_{3}S}{{T}_{3}}$
��ã�${L}_{3}=\frac{{T}_{3}}{{T}_{2}}{L}_{2}=\frac{300}{360}��54cm=45cm$
�𣺢ٻ�����Ҫ�뿪������ʱ���������¶�Ϊ87�棻
�ڷ�������¶��½���t3=27��ʱ���������ײ�֮��ľ���Ϊ45cm��
���� ���⿼������ʵ�鶨�ɣ��ؼ��Ǹ�������������仯���������������ֱ仯��Ȼ��ѡ����ʵ�����ʵ�鶨����ʽ��⼴�ɣ�

��ϰ��ϵ�д�
�����Ŀ
15�� ��ͼ��ʾ�����Ϊ45���б�£���б�µ�P�����Ϸ�ijһλ��Q�����ٶ�v0ˮƽ�����׳�һ��С��A��С��ǡ���ܴ�ֱ����б���ϣ��˶�ʱ��Ϊt1��С��B��ͬһ��Q���������䣬������P���ʱ��Ϊt2�����ƿ�����������t1��t2Ϊ��������
��ͼ��ʾ�����Ϊ45���б�£���б�µ�P�����Ϸ�ijһλ��Q�����ٶ�v0ˮƽ�����׳�һ��С��A��С��ǡ���ܴ�ֱ����б���ϣ��˶�ʱ��Ϊt1��С��B��ͬһ��Q���������䣬������P���ʱ��Ϊt2�����ƿ�����������t1��t2Ϊ��������
 ��ͼ��ʾ�����Ϊ45���б�£���б�µ�P�����Ϸ�ijһλ��Q�����ٶ�v0ˮƽ�����׳�һ��С��A��С��ǡ���ܴ�ֱ����б���ϣ��˶�ʱ��Ϊt1��С��B��ͬһ��Q���������䣬������P���ʱ��Ϊt2�����ƿ�����������t1��t2Ϊ��������
��ͼ��ʾ�����Ϊ45���б�£���б�µ�P�����Ϸ�ijһλ��Q�����ٶ�v0ˮƽ�����׳�һ��С��A��С��ǡ���ܴ�ֱ����б���ϣ��˶�ʱ��Ϊt1��С��B��ͬһ��Q���������䣬������P���ʱ��Ϊt2�����ƿ�����������t1��t2Ϊ��������| A�� | 1��2 | B�� | 1��$\sqrt{3}$ | C�� | 1��3 | D�� | 1��$\sqrt{2}$ |
20�� ��ͼ��ʾ�������ѹ��ԭ��Ȧ���н�����Դ������Ȧ��ͨ������߽��е���Ll��L2�ͺ�����о����ȦL������ߵ�Ч����ΪR����ʼʱ������S�Ͽ�����ƬP����ͼʾλ�ã�����L1�ܷ��⣮Ҫʹ����L1���������Բ�ȡ�İ취�ǣ�������
��ͼ��ʾ�������ѹ��ԭ��Ȧ���н�����Դ������Ȧ��ͨ������߽��е���Ll��L2�ͺ�����о����ȦL������ߵ�Ч����ΪR����ʼʱ������S�Ͽ�����ƬP����ͼʾλ�ã�����L1�ܷ��⣮Ҫʹ����L1���������Բ�ȡ�İ취�ǣ�������
 ��ͼ��ʾ�������ѹ��ԭ��Ȧ���н�����Դ������Ȧ��ͨ������߽��е���Ll��L2�ͺ�����о����ȦL������ߵ�Ч����ΪR����ʼʱ������S�Ͽ�����ƬP����ͼʾλ�ã�����L1�ܷ��⣮Ҫʹ����L1���������Բ�ȡ�İ취�ǣ�������
��ͼ��ʾ�������ѹ��ԭ��Ȧ���н�����Դ������Ȧ��ͨ������߽��е���Ll��L2�ͺ�����о����ȦL������ߵ�Ч����ΪR����ʼʱ������S�Ͽ�����ƬP����ͼʾλ�ã�����L1�ܷ��⣮Ҫʹ����L1���������Բ�ȡ�İ취�ǣ�������| A�� | ���ϻ���P | B�� | �պϿ���S | ||
| C�� | �����Ȧ�е���о | D�� | ��������Դ��Ƶ�� |
17��˫��ϵͳ�����ź�����ɣ���������������������£��ֱ�Χ���������ϵ�ijһ����������ͬ������Բ���˶����о����֣�˫��ϵͳ�ݻ������У����ǵ�������?��������ھ����ܷ����仯����ij˫��ϵͳ��������Բ���˶�������ΪT������һ��ʱ���ݻ���������������Ϊԭ����k��������֮��ľ����Ϊԭ����n�������ʱԲ���˶�������Ϊ��������
| A�� | $\sqrt{\frac{n}{k}}$T | B�� | $\sqrt{\frac{{n}^{2}}{k}}$T | C�� | $\sqrt{\frac{{n}^{3}}{{k}^{2}}}$T | D�� | $\sqrt{\frac{{n}^{3}}{k}}$T |
15������˵������ȷ���ǣ�������
| A�� | ����ʿ������ʱʹ�ñ㲽����Ϊ�˷�ֹ�ŷ����������� | |
| B�� | ��е���͵�Ų��ڽ����еĴ����ٶȽ��ɽ��ʾ��� | |
| C�� | ���������ǹ�ͨ��Բ��������ʱ�γɵ� | |
| D�� | ���㲣�������ڵ���Ʒʱ���ھ�ͷǰ��װһ��ƫ��Ƭ�Լ��������ķ���� |
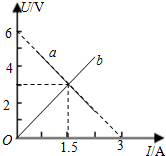 ��ͼ��ʾ��a��ij��Դ��U?Iͼ�ߣ�b�ǵ���R��U?Iͼ�ߣ���ͼ��֪�����Դ�ĵ綯�Ƶ���6V������������Դ���������R�����ɱպϵ�·����ñպϻ�·�ĵ�����С����1.5A��
��ͼ��ʾ��a��ij��Դ��U?Iͼ�ߣ�b�ǵ���R��U?Iͼ�ߣ���ͼ��֪�����Դ�ĵ綯�Ƶ���6V������������Դ���������R�����ɱպϵ�·����ñպϻ�·�ĵ�����С����1.5A�� ��ͼ��ʾ���뾶ΪR��Բ�ε������ġ����ٴ����뾶ҲΪR��Բ����ǿ�ų����涨��ʱ�뷽��ĸ�Ӧ����Ϊ���������и�Ӧ����i��ʱ��t�ı仯��ϵͼ�������ʵ�ʵ��ǣ�������
��ͼ��ʾ���뾶ΪR��Բ�ε������ġ����ٴ����뾶ҲΪR��Բ����ǿ�ų����涨��ʱ�뷽��ĸ�Ӧ����Ϊ���������и�Ӧ����i��ʱ��t�ı仯��ϵͼ�������ʵ�ʵ��ǣ�������



 ��ͼ��ʾ���⻬ˮƽ���ϻ���A��C'������Ϊm=1kg��B����ΪM=3kg����ʼʱA��B��ֹ��C���Գ��ٶ�v0=2m/s���ٶȻ���A����A����C���ٶȱ�Ϊ�㣬A�����˶���B������ײ��ճ��һ��
��ͼ��ʾ���⻬ˮƽ���ϻ���A��C'������Ϊm=1kg��B����ΪM=3kg����ʼʱA��B��ֹ��C���Գ��ٶ�v0=2m/s���ٶȻ���A����A����C���ٶȱ�Ϊ�㣬A�����˶���B������ײ��ճ��һ��