题目内容
如图所示,一束激光从O 点由空气射入厚度均匀的介质,经下表面反射后,从上的 A 点射出;已知入射角为 θ 1,A 与 O 相距 l,介质的折射率为 n,光在空气中的传播速度为 c.试求光在介质中的传播时间 t.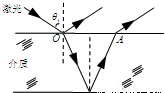
【答案】分析:由题已知入射角为θ1和折射率n,根据折射定律求出光在介质上界面的折射角θ2,由几何关系求出光在介质中传播的路程,由v=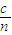 求出光在介质中传播速度.光在介质中传播的速度大小不变,再求出光在介质中的传播时间t.
求出光在介质中传播速度.光在介质中传播的速度大小不变,再求出光在介质中的传播时间t.
解答:解:设光在介质中传播的路程为2x,在OA面折射角为θ2.
根据折射定律得n=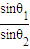
图中sinθ2=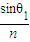
由几何关系得x=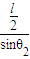 =
=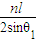
光在介质中传播速度为v=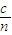
故光在介质中的传播时间 t=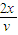 =
=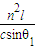 .
.
答:光在介质中的传播时间t=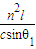 .
.
点评:本题是折射定律与几何知识的综合应用,抓住入射角、折射角、折射率、光速等各个量的关系研究,是这类问题解答的基础.
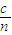 求出光在介质中传播速度.光在介质中传播的速度大小不变,再求出光在介质中的传播时间t.
求出光在介质中传播速度.光在介质中传播的速度大小不变,再求出光在介质中的传播时间t.解答:解:设光在介质中传播的路程为2x,在OA面折射角为θ2.
根据折射定律得n=
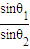
图中sinθ2=
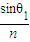
由几何关系得x=
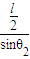 =
=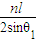
光在介质中传播速度为v=
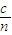
故光在介质中的传播时间 t=
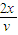 =
=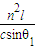 .
.答:光在介质中的传播时间t=
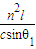 .
.点评:本题是折射定律与几何知识的综合应用,抓住入射角、折射角、折射率、光速等各个量的关系研究,是这类问题解答的基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,一束激光从O 点由空气射入厚度均匀的介质,经下表面反射后,从上的 A 点射出;已知入射角为 θ 1,A 与 O 相距 l,介质的折射率为 n,光在空气中的传播速度为 c.试求光在介质中的传播时间 t.
如图所示,一束激光从O 点由空气射入厚度均匀的介质,经下表面反射后,从上的 A 点射出;已知入射角为 θ 1,A 与 O 相距 l,介质的折射率为 n,光在空气中的传播速度为 c.试求光在介质中的传播时间 t. 如图所示,一束激光从O点由空气射入厚度均匀的介质,经下表面反射后,从上面的A点射出.已知入射角为i,A与O相距l,介质的折射率为n,试求介质的厚度d.
如图所示,一束激光从O点由空气射入厚度均匀的介质,经下表面反射后,从上面的A点射出.已知入射角为i,A与O相距l,介质的折射率为n,试求介质的厚度d.
