题目内容
1.在以加速度a=5m/s2匀加速上升的飞船上,由于超重现象,某时刻用弹簧秤测量质量为10kg的物体的重力时,弹簧秤的示数仅为75N,由此可知,此时飞船所处的位置距地球表面高度为多少km(g=10m/s2为地表附近重力加速度,地球半径为6400km).分析 根据牛顿第二定律求出火箭所在位置的重力加速度,结合万有引力等于重力求出火箭距离地面的高度.
解答 解:根据牛顿第二定律得:
F-mg′=ma,
解得:
g′=$\frac{F-ma}{m}$=$\frac{75-10×5}{10}$m/s2=2.5m/s2,
根据G$\frac{Mm}{{R}^{2}}$=mg,G$\frac{Mm}{(R+h)^{2}}$=mg′,
联立两式解得:
h=R=6400km.
答:该时刻火箭距地面的高度为6400km.
点评 此题考查万有引力定律、牛顿运动定律,要掌握重力等于万有引力这个关系.并能灵活运用,难度不大.

练习册系列答案
相关题目
11. 如图所示,图线a是线圈在匀强磁场中匀速转动时所产生正弦交流电的图象,当调整线圈转速后,所产生正弦交流电的图象如图线b所示,以下关于这两个正弦交流电的说法正确的是( )
如图所示,图线a是线圈在匀强磁场中匀速转动时所产生正弦交流电的图象,当调整线圈转速后,所产生正弦交流电的图象如图线b所示,以下关于这两个正弦交流电的说法正确的是( )
 如图所示,图线a是线圈在匀强磁场中匀速转动时所产生正弦交流电的图象,当调整线圈转速后,所产生正弦交流电的图象如图线b所示,以下关于这两个正弦交流电的说法正确的是( )
如图所示,图线a是线圈在匀强磁场中匀速转动时所产生正弦交流电的图象,当调整线圈转速后,所产生正弦交流电的图象如图线b所示,以下关于这两个正弦交流电的说法正确的是( )| A. | 在图中t=0时刻穿过线圈的磁通量均为零 | |
| B. | 线圈先、后两次转速之比为3:2 | |
| C. | 交流电a的瞬时值表达式为u=10sin 5πt (V) | |
| D. | 交流电b的最大值为5 V |
12.关于牛顿第三定律,下列说法正确是( )
| A. | 牛顿第三定律在物体处于非平衡状态时也适用 | |
| B. | 作用力和反作用力是作用在同一个物体上的 | |
| C. | 作用力和反作用力的方向总是相反的 | |
| D. | 作用力大时,反作用力小 |
9.我国的“北斗一号”卫星定位系统由三颗卫星组成,三颗卫星都定位在距地面约36000km的地球同步轨道上.美国的全球卫星定位系统(简称GPS)由24颗卫星组成,这些卫星距地面的高度均约为20000km.比较这些卫星,下列说法中正确的是( )
| A. | “北斗一号”系统中的三颗卫星的质量必须相同,否则它们不能定位在同一轨道上 | |
| B. | “北斗一号”卫星的周期比GPS卫星的周期短 | |
| C. | “北斗一号”卫星的加速度比GPS卫星的加速度小 | |
| D. | “北斗一号”卫星的运行速度比GPS卫星的运行速度小 |
6.在“测定匀变速直线运动的加速度”的实验中,如果电源的频率稍微减小从而导致打点的周期稍微变大了一点,而实验者并不知情,则( )
| A. | 它将导致实验者测量的相邻计数点之间的间隔变大,从而使测得的加速度偏大 | |
| B. | 它将导致实验者用公式vn=$\frac{{x}_{n}+{x}_{n+1}}{2T}$求得的各计数点对应的瞬时速度偏大,从而用v-t图象处理数据时导致测得的加速度偏大 | |
| C. | 它将导致实验者用公式vn=$\frac{{x}_{n}+{x}_{n+1}}{2T}$求得的各计数点对应的瞬时速度偏小,从而用v-t图象处理数据时导致测得的加速度偏小 | |
| D. | 用逐差法处理数据时,由于代入的T的数据偏小,从而导致测得的加速度偏大 |
13.一条河宽100米,船在静水中的速度为4m/s,水流速度是5m/s,则( )
| A. | 该船可以垂直河岸横渡到正对岸 | |
| B. | 当船头垂直河岸横渡时,过河所用的时间最短 | |
| C. | 当船头垂直河岸横渡时,过河位移最小 | |
| D. | 该船横渡到对岸的最小位移是100米 |
15. 自行车上的红色尾灯不仅是装饰品,也是夜间骑车的安全指示灯,它能把来自后面的光照反射回去.某种自行车尾灯可简化为由许多整齐排列的等腰直角棱镜(折射率n>$\sqrt{2}$)组成,棱镜的横截面如图所示.一平行于横截面的光线从O点垂AB边射入棱镜,先后经过AC边和BC边反射后,从AB边的O′点射出,则出射光线是( )
自行车上的红色尾灯不仅是装饰品,也是夜间骑车的安全指示灯,它能把来自后面的光照反射回去.某种自行车尾灯可简化为由许多整齐排列的等腰直角棱镜(折射率n>$\sqrt{2}$)组成,棱镜的横截面如图所示.一平行于横截面的光线从O点垂AB边射入棱镜,先后经过AC边和BC边反射后,从AB边的O′点射出,则出射光线是( )
 自行车上的红色尾灯不仅是装饰品,也是夜间骑车的安全指示灯,它能把来自后面的光照反射回去.某种自行车尾灯可简化为由许多整齐排列的等腰直角棱镜(折射率n>$\sqrt{2}$)组成,棱镜的横截面如图所示.一平行于横截面的光线从O点垂AB边射入棱镜,先后经过AC边和BC边反射后,从AB边的O′点射出,则出射光线是( )
自行车上的红色尾灯不仅是装饰品,也是夜间骑车的安全指示灯,它能把来自后面的光照反射回去.某种自行车尾灯可简化为由许多整齐排列的等腰直角棱镜(折射率n>$\sqrt{2}$)组成,棱镜的横截面如图所示.一平行于横截面的光线从O点垂AB边射入棱镜,先后经过AC边和BC边反射后,从AB边的O′点射出,则出射光线是( )| A. | 平行于AC边的光线① | B. | 平行于入射光线的光线② | ||
| C. | 平行于BC边的光线③ | D. | 平行于AB边的光线④ |

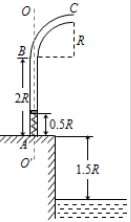 如图为某种鱼饵自动投放器中的投饵管装置示意图,上半部BC是半径为R的四分之一圆弧弯管,管口C处的切线沿水平方向,其下半部AB是一长为2R的竖直细管,AB管内有一原长为R、下端固定的轻质弹簧.投饵时,每次总将弹簧长度压缩到0.5R后锁定,在弹簧上端放置一粒鱼饵,解除锁定,弹簧可将鱼饵弹射出去.设质量为m的鱼饵到达管口C时,对管壁的作用力恰好为零.不计鱼饵在运动过程中的机械能损失,且锁定和解除锁定时,均不改变弹簧的弹性势能.已知重力加速度为g.求:
如图为某种鱼饵自动投放器中的投饵管装置示意图,上半部BC是半径为R的四分之一圆弧弯管,管口C处的切线沿水平方向,其下半部AB是一长为2R的竖直细管,AB管内有一原长为R、下端固定的轻质弹簧.投饵时,每次总将弹簧长度压缩到0.5R后锁定,在弹簧上端放置一粒鱼饵,解除锁定,弹簧可将鱼饵弹射出去.设质量为m的鱼饵到达管口C时,对管壁的作用力恰好为零.不计鱼饵在运动过程中的机械能损失,且锁定和解除锁定时,均不改变弹簧的弹性势能.已知重力加速度为g.求: