题目内容
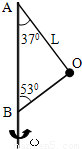
如图所示，OA、OB两根绳子系着一个质量为m=0.5Kg的小球，两绳的A、B端分别固定在竖直转动轴上，OA绳长L=2m，两绳都拉直时与轴的夹角分别为37和53，（sin37°=0.6 cos37°=0.8 g=10m/s2） 求：（1）小球随轴转动的角速度ω=2.4rad/s时，绳OA、OB的张力分别是多少？
（2）小球随轴转动的角速度ω=3.0rad/s时，绳OA、OB的张力分别是多少？
【答案】分析：若转速为零，则AO绳子竖直；首先求解OB绳子刚好拉直时的角速度，然后将已知角速度与临界角速度相比较，运用牛顿第二定律列式求解．
解答：解：（1）若OB绳子刚好伸直，则：
mgtan37°=m（Lsin37°）ω2
解得：ω=2.5rad/s
当ω=2.4rad/s＜ω时，OB绳子是弯曲的；
故OB绳子张力为零；
根据牛顿第二定律，有：
TOAx=m（Lsin37°）ω2=3.456N；
TOAy=mg=5N；
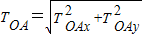≈6.1N；
（2）当ω=3.0rad/s＞ω时，OB绳子是伸直的，根据牛顿第二定律，有
水平方向：TOAcos37°-TOBcos53°-mg=0
竖直方向：TOAsin37°+TOBcos37°=m（Lsin37°）ω2
解得：TOA=7.24N
TOB=1.32N
（1）小球随轴转动的角速度ω=2.4rad/s时，绳OA的张力是6.1N，OB的张力为零；
（2）小球随轴转动的角速度ω=3.0rad/s时，绳OA的张力是7.24N，OB的张力为1.32N．
点评：本题关键是要找出绳子OB恰好拉直的临界状态，然后根据牛顿第二定律列式求解．
解答：解：（1）若OB绳子刚好伸直，则：
mgtan37°=m（Lsin37°）ω2
解得：ω=2.5rad/s
当ω=2.4rad/s＜ω时，OB绳子是弯曲的；
故OB绳子张力为零；
根据牛顿第二定律，有：
TOAx=m（Lsin37°）ω2=3.456N；
TOAy=mg=5N；
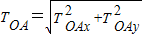≈6.1N；（2）当ω=3.0rad/s＞ω时，OB绳子是伸直的，根据牛顿第二定律，有
水平方向：TOAcos37°-TOBcos53°-mg=0
竖直方向：TOAsin37°+TOBcos37°=m（Lsin37°）ω2
解得：TOA=7.24N
TOB=1.32N
（1）小球随轴转动的角速度ω=2.4rad/s时，绳OA的张力是6.1N，OB的张力为零；
（2）小球随轴转动的角速度ω=3.0rad/s时，绳OA的张力是7.24N，OB的张力为1.32N．
点评：本题关键是要找出绳子OB恰好拉直的临界状态，然后根据牛顿第二定律列式求解．
练习册系列答案
相关题目
如图所示，OA、OB、OC三段轻绳结于O点，下方轻绳OC悬挂质量为m1=0.3kg的物体甲．轻绳OB水平，B端与放置在水平面上的质量为m2=2kg的物体乙相连，物体乙恰好处于静止状态，已知物体乙与地面间的动摩擦因数为μ=0.2，重力加速度g取10m/s2，可认为最大静摩擦力与滑动摩擦力相等．求：
如图所示，oa、ob、oc是竖直面内三根固定的光滑细杆，O、a、b、c、d位于同一圆周上，d点为圆周的最高点，c点为最低点．每根杆上都套着一个小滑环（图中未画出），三个滑环都从o点无初速释放，用t1、t2、t3依次表示滑环到达a、b、c所用的时间，则（ ）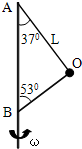
如图所示，OA、OB两根绳子系着一个质量为m=0.5Kg的小球，两绳的A、B端分别固定在竖直转动轴上，OA绳长L=2m，两绳都拉直时与轴的夹角分别为370和530，（sin37°=0.6 cos37°=0.8 g=10m/s2） 求：
（2012?上海模拟）如图所示，OA、OB是竖直面内两根固定的光滑细杆，O、A、B、C位于同一圆周上，C点为圆周的最高点，B点为最低点．每根杆上都套着一个小滑环（图中未画出），两个滑环都从O点无初速释放，用t1、t2分别表示滑环到达A、B所用的时间，则（ ）
两物体M、m用跨过光滑定滑轮的轻绳相连，如图所示，OA、OB与水平面的夹角分别为30°、60°，M、m均处于静止状态．则（ ）| A、绳OA的拉力大于绳OB的拉力 | B、绳OA的拉力小于绳OB的拉力 | C、m受到水平面的静摩擦力的方向水平向左 | D、m受到水平面的静摩擦力的方向水平向右 |