题目内容
1966年曾在地球的上空完成了以牛顿第二定律为基础的测定质量的实验．实验时，用宇宙飞船（质量为m）去接触正在轨道上运行的火箭（质量为mx，发动机已熄火），如图所示．接触以后，开动飞船尾部的推进器，使飞船和火箭共同加速，推进器的平均推力为F，开动时间△t，测出飞船和火箭的速度变化是△v，下列说法正确的是（ ）
A．火箭质量mx应为
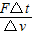
B．宇宙飞船的质量m应为
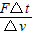
C．推力F越大，
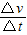就越大，且
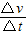与F成正比D．推力F通过飞船传递给火箭，所以飞船对火箭的弹力大小应为F
【答案】分析：对整体由动量定理可得出速度变化、质量及力之间的关系，分析各项即可得出正确结论．
解答：解：对整体由动量定理可得：F△t=（m+mx）△v；
A、火箭的质量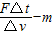
．整体的质量为
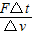．故A、B错误．
C、由公式可得，F=（m+mx）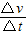
可知，推力F越大，
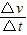就越大，且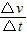
与F成正比．故C正确．
D、隔离对mx分析，根据牛顿第二定律有：N=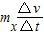
＜F．故D错误．
故选C．
点评：本题也可以通过牛顿第二定律得出正确结果，但很明显动量定理更便捷一些，可以在一些和时间有关的动力学题目中应用动量定理求解．
解答：解：对整体由动量定理可得：F△t=（m+mx）△v；
A、火箭的质量
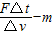．整体的质量为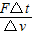．故A、B错误．C、由公式可得，F=（m+mx）
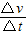可知，推力F越大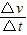，就越大，且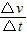与F成正比．故C正确．D、隔离对mx分析，根据牛顿第二定律有：N=
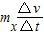＜F．故D错误．故选C．
点评：本题也可以通过牛顿第二定律得出正确结果，但很明显动量定理更便捷一些，可以在一些和时间有关的动力学题目中应用动量定理求解．
练习册系列答案
相关题目
1966年曾在地球的上空完成了以牛顿第二定律为基础的测定质量的实验．实验时，用双子星号宇宙飞船m1，去接触正在轨道上运行的火箭组m2，接触以后，开动飞船尾部的推进器，使飞船和火箭组共同加速（如图所示）．推进器的平均作用力F等于895N，推进器开动7s，测出飞船和火箭组的速度改变是0.91m/s．已知双子星号宇宙飞船的质量m1=3400kg．求：
力学问题中，如果知道物体的受力情况和加速度，就可以测出物体的质量，就是说，质量可以用动力学的方法来测定．下面是用动力学的方法测定质量的一个有趣的题目：1966年曾在地球的上空完成了以牛顿第二定律为基础的测定质量的实验．实验时，用双子星号宇宙飞船m1，去接触正在轨道上运行的火箭组m2，接触后，开动飞船尾部的推进器，使飞船和火箭共同加速（如图）．推进器的平均推力F等于895N，推进器开动7s，测出飞船和火箭组的速度改变是0.91m/s，已知双子星号宇宙飞船的质量m1=3400kg．求火箭组的质量m2多大？
1966年曾在地球的上空完成了以牛顿第二定律为基础的测定质量的实验，实验时，用宇宙飞船（质量m）去接触正在轨道上运行的火箭（质量mx，发动机已熄火），如图所示，接触以后，开动飞船尾部的推进器，使飞船和火箭组共同加速，推进器的平均推力为F，开动时间△t，测出飞船和火箭组的速度变化是△v，下列说法正确的是（ ）
应为
就越大，且