题目内容
（7分）如图12所示，水平桌面上放置一个质量m＝0.5kg的小木块，若用木棒击打木块使木块获得水平方向的初速度v0，木块沿桌面滑出左端边沿，落在水平地面上的D点。已知木块的初速度v0＝5.0m/s，桌面距地面的高度H＝0.8m，木块落地的位置距桌面左端边沿的水平距离x＝1.2m，忽略空气阻力，取重力加速度g＝10m/s2。求：
（1）木块落到地面时的速度大小；
（2）木块离开桌面时的动能；
（3）木块在桌面上滑行过程中克服摩擦力
所做的功。
解：（1）木块离开桌面后做平抛运动，设运动时间为t，根据自由落体公式
木块做平抛运动的时间 
＝0.4s
木块落地时沿水平方向的分速度 vx=
=3.0 m/s （1分）
根据动能公式，得木块离开桌面时的动能
＝2.25 J （2分）
（2）木块落地时沿竖直方向的分速度 vy=gt＝4.0 m/s （1分）
木块落到地面时的速度大小 
＝5.0 m/s （1分）
（3）根据动能定理
W＝
＝4.0 J （2分）
如图12所示质量为M的小物块A静止在离地面高h的水平桌面的边缘，质量为m的小物块B沿桌面向A运动并以速度v0与之发生正碰（碰撞时间极短）．碰后A离开桌面，其落点离出发点的水平距离为L．碰后B反向运动．已知B与桌面的动摩擦因数为μ，重力加速度为g，桌面足够长．
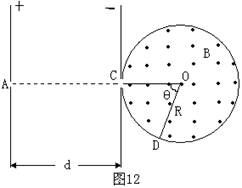（06年广东卷）（17 分）在光滑绝缘的水平桌面上，有两个质量均为m，电量为＋q的完全相同的带电粒子P1和P2，在小孔A处以初速度为零先后释放。在平行板间距为d的匀强电场中加速后，P1从C处对着圆心进入半径为R的固定圆筒中（筒壁上的小孔C只能容一个粒子通过），圆筒内有垂直水平面向上的磁感应强度为B的匀强磁场。P1每次与筒壁发生碰撞均无电荷迁移，P1进入磁场第一次与筒壁碰撞点为D，∠COD=θ，如图12所示。延后释放的P2，将第一次欲逃逸出圆筒的P1正碰圆筒内，此次碰撞刚结束，立即改变平行板间的电压，并利用P2与P1之后的碰撞，将P1限制在圆筒内运动。碰撞过程均无机械能损失。设d=
，求：在P2和P1相邻两次碰撞时间间隔内，粒子P1与筒壁的可能碰撞次数。
附：部分三角函数值
|
|
|
|
|
|
|
|
|
|
tan | 3.08 | 1.37 | 1.00 | 0.73 | 0.58 | 0.48 | 0.41 | 0.36 | 0.32 |
如图12所示质量为M的小物块A静止在离地面高h的水平桌面的边缘，质量为m的小物块B沿桌面向A运动并以速度v0与之发生正碰（碰撞时间极短）。碰后A离开桌面，其落点离出发点的水平距离为L。碰后B反向运动。已知B与桌面的动摩擦因数为μ，重力加速度为g，桌面足够长。
一些点.已知打点计时器所用交流电源的频率为50 Hz(打点计时器每隔0.02 s打一个点),利用图中给出的数据,算出打点计时器打下B点时小车的速度大小vB=_____m/s,小车运动过程中的加速度大小a=_____m/s2.(结果均保留3位有效数字)
